题目内容
已知f(x)=x2+bx+c(b,c∈R),g(x)=4-x-m•(2-x)-9(m∈R),A={x|f(x)=x-2}.
(1)若A={1},解不等式f(x)>1;
(2)若b∈Z,-3∈A,x1,x2为方程f(x)=0的两个实根,且
+
=-
,
①求b,c的值
②若对任意的t1∈[-2,2],总存在t2∈[-2,2],使得f(t1)=g(t2)成立,求m的取值范围.
(1)若A={1},解不等式f(x)>1;
(2)若b∈Z,-3∈A,x1,x2为方程f(x)=0的两个实根,且
| 4 |
| x1 |
| 1 |
| x2 |
| 1 |
| 2 |
①求b,c的值
②若对任意的t1∈[-2,2],总存在t2∈[-2,2],使得f(t1)=g(t2)成立,求m的取值范围.
考点:二次函数的性质,一元二次不等式的解法
专题:函数的性质及应用
分析:(1)根据已知条件即可得到1是方程x2+(b-1)x+c+2=0的二重根,所以由韦达定理即可求出b,c,从而解出不等式f(x)>1;
(2)①先由-3∈A便容易得到c=3b-14,而根据韦达定理及求根公式可得到
,所以
+
=
=
=-
,所以联立c=3b-14即可求出b=2,c=-8;
②根据条件即知f(x)在[-2,2]上的值域是g(x)在[-2,2]上的子集,容易求出f(x)在[-2,2]上的值域为[-9,0].换元,令2-x=t,t∈[
,4],所以得到一个关于t二次函数h(t)=t2-mt-9,所以根据二次函数的单调性及取得顶点情况讨论m的取值,求出每个m取值下的h(t)的值域,使该值域包含区间[-9,0],从而能得到m的取值范围.
(2)①先由-3∈A便容易得到c=3b-14,而根据韦达定理及求根公式可得到
|
| 4 |
| x1 |
| 1 |
| x2 |
| 3x2+x1+x2 |
| x1x2 |
| ||||
| c |
| 1 |
| 2 |
②根据条件即知f(x)在[-2,2]上的值域是g(x)在[-2,2]上的子集,容易求出f(x)在[-2,2]上的值域为[-9,0].换元,令2-x=t,t∈[
| 1 |
| 4 |
解答:
解:(1)A={x|x2+(b-1)x+c+2=0};
∵A={1};
∴1是方程x2+(b-1)x+c+2=0的二重根;
∴
;
∴b=-1,c=-1;
∴由f(x)>1得,x2-x-2>0,解得:x<-1,或x>2;
∴f(x)>1的解为{x|x<-1,或x>2};
(2)①-3∈A;
∴-3b+c+14=0;
∴c=3b-14;
x1,x2是方程f(x)=0的两个根;
∴
;
∴
+
=
=
=-
;
整理成:±3
=5b-c;
∴将c=3b-14带入上式可得,±3
=2b+14;
∴对上式两边平方并整理可得:5b2-164b+308=0;
解得b=2,或
(舍去);
∴c=-8;
②f(x)=x2+2x-8;
由②中的条件知,f(x)在[-2,2]上的值域是g(x)在[-2,2]上值域的子集;
f(x)=(x+1)2-9;
∴f(x)在[-2,2]上的值域为[f(-1),f(2)]=[-9,0];
设2-x=t(t∈[
,4]),h(t)=t2-mt-9;
∴函数h(t)的对称轴为t=
;
(一)若
<
,即m<
,h(t)在[
,4]上单调递增;
∴h(t)在[
,4]上的值域为[h(
),h(4)]=[-
m-
,-4m+7];
∴
,解得
≤m≤
;
∴
≤m<
;
(二)若
≤
≤4,即
≤m≤2,则:h(
),h(4)中必有一个为h(t)在[
,4]上的最大值,最小值为h(
)=-
-9;
显然最小值-
-9≤-9,所以只需满足-
m-
≥0,或-4m+7≥0;
∴m≤
,或m≤-
(舍去);
∴
≤m≤
;
(三)若
>4,即m>8,h(t)在[
,4]上单调递减;
∴h(t)的值域为[h(4),h(
)]=[-4m+7,-
m-
];
∴
;
解得m∈∅;
∴综上得m的取值范围为[
,
].
∵A={1};
∴1是方程x2+(b-1)x+c+2=0的二重根;
∴
|
∴b=-1,c=-1;
∴由f(x)>1得,x2-x-2>0,解得:x<-1,或x>2;
∴f(x)>1的解为{x|x<-1,或x>2};
(2)①-3∈A;
∴-3b+c+14=0;
∴c=3b-14;
x1,x2是方程f(x)=0的两个根;
∴
|
∴
| 4 |
| x1 |
| 1 |
| x2 |
| 3x2+x1+x2 |
| x1x2 |
| ||||
| c |
| 1 |
| 2 |
整理成:±3
| b2-4c |
∴将c=3b-14带入上式可得,±3
| b2-12b+56 |
∴对上式两边平方并整理可得:5b2-164b+308=0;
解得b=2,或
| 154 |
| 5 |
∴c=-8;
②f(x)=x2+2x-8;
由②中的条件知,f(x)在[-2,2]上的值域是g(x)在[-2,2]上值域的子集;
f(x)=(x+1)2-9;
∴f(x)在[-2,2]上的值域为[f(-1),f(2)]=[-9,0];
设2-x=t(t∈[
| 1 |
| 4 |
∴函数h(t)的对称轴为t=
| m |
| 2 |
(一)若
| m |
| 2 |
| 1 |
| 4 |
| 1 |
| 2 |
| 1 |
| 4 |
∴h(t)在[
| 1 |
| 4 |
| 1 |
| 4 |
| 1 |
| 4 |
| 143 |
| 16 |
∴
|
| 1 |
| 4 |
| 7 |
| 4 |
∴
| 1 |
| 4 |
| 1 |
| 2 |
(二)若
| 1 |
| 4 |
| m |
| 2 |
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 4 |
| m |
| 2 |
| m2 |
| 4 |
显然最小值-
| m2 |
| 4 |
| 1 |
| 4 |
| 143 |
| 16 |
∴m≤
| 7 |
| 4 |
| 143 |
| 4 |
∴
| 1 |
| 2 |
| 7 |
| 4 |
(三)若
| m |
| 2 |
| 1 |
| 4 |
∴h(t)的值域为[h(4),h(
| 1 |
| 4 |
| 1 |
| 4 |
| 143 |
| 16 |
∴
|
解得m∈∅;
∴综上得m的取值范围为[
| 1 |
| 4 |
| 7 |
| 4 |
点评:考查描述法表示集合,韦达定理,以及解一元二次不等式,一元二次方程的求根公式,换元法求函数的值域,二次函数的单调性及二次函数在闭区间上值域的求法.

练习册系列答案
相关题目
函数y=
的定义域为( )
| 2-2x |
| A、[0,+∞) |
| B、[1,+∞) |
| C、(-∞,0] |
| D、(-∞,1] |
已知sin(-α)=
,α∈(-
,0),则tanα等于( )
2
| ||
| 3 |
| π |
| 2 |
A、
| ||||
B、-
| ||||
C、2
| ||||
D、-2
|
i是虚数单位,复数i2(i-1)的虚部是( )
| A、i | B、-i | C、1 | D、-1 |
直线bx-ay+c=0(a>0)是曲线y=ln
在x=3处的切线,f(x)=a•2x+b•3x,若f(x+1)>f(x),则x的取值范围是( )
| 1 |
| x |
| A、(-2,1) |
| B、(1,+∞) |
| C、(-∞,1) |
| D、(-2,-1) |
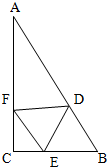 某个公园有个池塘,其形状为直角△ABC,∠C=90°,AB=200米,BC=100米.现在准备新建造一个荷塘,分别在AB,BC,CA上取点D,E,F,建造△DEF连廊(不考虑宽度)供游客休憩,且使△DEF为正三角形,设求△DEF边长的最小值.
某个公园有个池塘,其形状为直角△ABC,∠C=90°,AB=200米,BC=100米.现在准备新建造一个荷塘,分别在AB,BC,CA上取点D,E,F,建造△DEF连廊(不考虑宽度)供游客休憩,且使△DEF为正三角形,设求△DEF边长的最小值.