题目内容
在数列{an}中,a1=14,3an=3an+1+2,则使anan+2<0成立的n值是( )
| A、21 | B、22 | C、23 | D、24 |
考点:等差数列的通项公式
专题:等差数列与等比数列
分析:先由已知的递推式得到an+1-an=-
,判断出数列为等差数列,进而求得数列的通项公式,根据anan+2<0求得an的范围,则n的值可得.
| 2 |
| 3 |
解答:
解:∵3an=3an+1+2,
∴an+1-an=-
,
∴数列{an}是以14为首项,-
为公差的等差数列,
∴an=14-(n-1)×
=
-
n,
∵anan+2<0,即an(an-
)<0
∴0<an<
,即0<
-
n<
,
解得20<n<22
∴n的值是21.
故选:A.
∴an+1-an=-
| 2 |
| 3 |
∴数列{an}是以14为首项,-
| 2 |
| 3 |
∴an=14-(n-1)×
| 2 |
| 3 |
| 44 |
| 3 |
| 2 |
| 3 |
∵anan+2<0,即an(an-
| 4 |
| 3 |
∴0<an<
| 4 |
| 3 |
| 44 |
| 3 |
| 2 |
| 3 |
| 4 |
| 3 |
解得20<n<22
∴n的值是21.
故选:A.
点评:本题主要考查了等差数列的通项公式.数列问题常与不等式,函数问题一块考查,应加强这方面的练习,是基础题.

练习册系列答案
相关题目
若实数x,y满足件
,则2x+y的最小值是( )
|
| A、-1 | ||
B、-
| ||
| C、0 | ||
| D、2 |
下列命题中,真命题是( )
| A、?x∈R,x2>0 |
| B、?x0∈R,x02-x0+1=0 |
| C、24是3的倍数且是9的倍数 |
| D、“若b=0,则函数f(x)=ax2+bx+c为偶函数”的逆否命题 |
函数y=
的定义域为( )
| 2-2x |
| A、[0,+∞) |
| B、[1,+∞) |
| C、(-∞,0] |
| D、(-∞,1] |
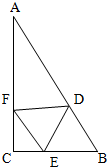 某个公园有个池塘,其形状为直角△ABC,∠C=90°,AB=200米,BC=100米.现在准备新建造一个荷塘,分别在AB,BC,CA上取点D,E,F,建造△DEF连廊(不考虑宽度)供游客休憩,且使△DEF为正三角形,设求△DEF边长的最小值.
某个公园有个池塘,其形状为直角△ABC,∠C=90°,AB=200米,BC=100米.现在准备新建造一个荷塘,分别在AB,BC,CA上取点D,E,F,建造△DEF连廊(不考虑宽度)供游客休憩,且使△DEF为正三角形,设求△DEF边长的最小值.