题目内容
设函数f(x)=cos2x-
sin2x,若α∈(
,
)且满足f(α)=
-
,求tan2α的值.
| ||
| 2 |
| π |
| 4 |
| π |
| 2 |
| 1 |
| 2 |
| ||
| 2 |
考点:三角函数中的恒等变换应用,二倍角的正切
专题:三角函数的求值
分析:利用二倍角的余弦与三角恒等变换可得f(x)=cos(2x+
)+
,依题意,可得cos(2α+
)=-
,2α+
∈(
,
),于是可求得2α=
,从而可得答案.
| π |
| 3 |
| 1 |
| 2 |
| π |
| 3 |
| ||
| 2 |
| π |
| 3 |
| 5π |
| 6 |
| 4π |
| 3 |
| 5π |
| 6 |
解答:
解:∵f(x)=cos2x-
sin2x=
-
sin2x=cos(2x+
)+
,
∴f(α)=cos(2α+
)+
=
-
,
∴cos(2α+
)=-
,
又α∈(
,
),2α+
∈(
,
),
∴2α+
=
,
∴2α=
,
∴tan2α=-
.
| ||
| 2 |
| 1+cos2x |
| 2 |
| ||
| 2 |
| π |
| 3 |
| 1 |
| 2 |
∴f(α)=cos(2α+
| π |
| 3 |
| 1 |
| 2 |
| 1 |
| 2 |
| ||
| 2 |
∴cos(2α+
| π |
| 3 |
| ||
| 2 |
又α∈(
| π |
| 4 |
| π |
| 2 |
| π |
| 3 |
| 5π |
| 6 |
| 4π |
| 3 |
∴2α+
| π |
| 3 |
| 7π |
| 6 |
∴2α=
| 5π |
| 6 |
∴tan2α=-
| ||
| 3 |
点评:本题考查三角函数中的恒等变换应用,考查余弦函数的图象与性质,求得cos(2α+
)=-
与2α+
∈(
,
)是关键,属于中档题.
| π |
| 3 |
| ||
| 2 |
| π |
| 3 |
| 5π |
| 6 |
| 4π |
| 3 |

练习册系列答案
 黄冈冠军课课练系列答案
黄冈冠军课课练系列答案 长江作业本同步练习册系列答案
长江作业本同步练习册系列答案
相关题目
i是虚数单位,复数i2(i-1)的虚部是( )
| A、i | B、-i | C、1 | D、-1 |
设a>0,f(x)=ex-
在任一点处的切线的倾斜角的取值范围是[
,
),则a=( )
| a |
| ex |
| π |
| 3 |
| π |
| 2 |
A、
| ||
B、
| ||
| C、3 | ||
D、
|
如果执行如图所示的程序框图,输入x=6,则输出的y值为( )


| A、2 | ||
| B、0 | ||
| C、-1 | ||
D、-
|
已知定义域为R的函数f(x)满足f(-x)=-f(x+4),且函数f(x)在区间(2,+∞)上单调递增.如果x1<2<x2,且x1+x2<4,则f(x1)+f(x2)的值( )
| A、可正可负 | B、恒大于0 |
| C、可能为0 | D、恒小于0 |
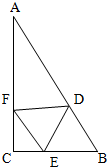 某个公园有个池塘,其形状为直角△ABC,∠C=90°,AB=200米,BC=100米.现在准备新建造一个荷塘,分别在AB,BC,CA上取点D,E,F,建造△DEF连廊(不考虑宽度)供游客休憩,且使△DEF为正三角形,设求△DEF边长的最小值.
某个公园有个池塘,其形状为直角△ABC,∠C=90°,AB=200米,BC=100米.现在准备新建造一个荷塘,分别在AB,BC,CA上取点D,E,F,建造△DEF连廊(不考虑宽度)供游客休憩,且使△DEF为正三角形,设求△DEF边长的最小值.