题目内容
已知两条不同的直线m,n和两个不同的平面α,β,以下四个结论中正确的个数为( )
①若m∥α,n∥β,且α∥β,则m∥n;
②若m∥α,n⊥β,且α⊥β,则m∥n;
③若m⊥α,n∥β,且α∥β,则m⊥n;
④若m⊥α,n⊥β,且α⊥β,则m⊥n.
①若m∥α,n∥β,且α∥β,则m∥n;
②若m∥α,n⊥β,且α⊥β,则m∥n;
③若m⊥α,n∥β,且α∥β,则m⊥n;
④若m⊥α,n⊥β,且α⊥β,则m⊥n.
| A、1个 | B、2个 | C、3个 | D、4个 |
考点:空间中直线与平面之间的位置关系
专题:空间位置关系与距离
分析:利用线面平行、面面平行以及线面垂直、面面垂直的性质对选项分别分析解答.
解答:
解:对于①,若m∥α,n∥β,且α∥β,则m∥n或者异面;故①错误;
对于②,若m∥α,n⊥β,且α⊥β,利用线面平行、线面垂直的性质,可得m与n平行或异面;故②不正确;
对于③,若m⊥α,n∥β,且α∥β,利用线面平行、线面垂直,面面平行的性质,可得m⊥n;正确
对于④,若m⊥α,n⊥β,且α⊥β,利用线面垂直、面面垂直的性质可得m⊥n.正确
故正确的有2个;
故选B.
对于②,若m∥α,n⊥β,且α⊥β,利用线面平行、线面垂直的性质,可得m与n平行或异面;故②不正确;
对于③,若m⊥α,n∥β,且α∥β,利用线面平行、线面垂直,面面平行的性质,可得m⊥n;正确
对于④,若m⊥α,n⊥β,且α⊥β,利用线面垂直、面面垂直的性质可得m⊥n.正确
故正确的有2个;
故选B.
点评:本题考查了线面平行、面面平行、线面垂直以及面面垂直的性质,熟练掌握定理是解答的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
i是虚数单位,复数i2(i-1)的虚部是( )
| A、i | B、-i | C、1 | D、-1 |
已知E,F分别为正方体ABCD-A1B1C1D的棱AB,AA1上的点,且AE=
AB,AF=
AA1,M,N分别为线段D1E和线段C1F上的点,则与平面ABCD平行的直线MN有( )
| 1 |
| 2 |
| 1 |
| 3 |
| A、1条 | B、3条 | C、6条 | D、无数条 |
设a>0,f(x)=ex-
在任一点处的切线的倾斜角的取值范围是[
,
),则a=( )
| a |
| ex |
| π |
| 3 |
| π |
| 2 |
A、
| ||
B、
| ||
| C、3 | ||
D、
|
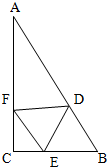 某个公园有个池塘,其形状为直角△ABC,∠C=90°,AB=200米,BC=100米.现在准备新建造一个荷塘,分别在AB,BC,CA上取点D,E,F,建造△DEF连廊(不考虑宽度)供游客休憩,且使△DEF为正三角形,设求△DEF边长的最小值.
某个公园有个池塘,其形状为直角△ABC,∠C=90°,AB=200米,BC=100米.现在准备新建造一个荷塘,分别在AB,BC,CA上取点D,E,F,建造△DEF连廊(不考虑宽度)供游客休憩,且使△DEF为正三角形,设求△DEF边长的最小值.