题目内容
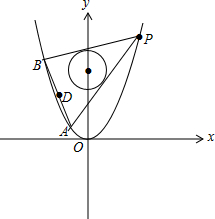
已知抛物线C1:x2=y,圆C2:x2+(y-4)2=1.
(1)在抛物线C1上取点M,C2的圆周取一点N,求|MN|的最小值;
(2)设P(x0,y0)(2≤x0≤4)为抛物线C1上的动点,过P作圆C2的两条切线,交抛物线C1于A,B两点.求AB的中点D的横坐标的取值范围.
(1)在抛物线C1上取点M,C2的圆周取一点N,求|MN|的最小值;
(2)设P(x0,y0)(2≤x0≤4)为抛物线C1上的动点,过P作圆C2的两条切线,交抛物线C1于A,B两点.求AB的中点D的横坐标的取值范围.
考点:圆与圆锥曲线的综合
专题:圆锥曲线的定义、性质与方程
分析:(1)设出M的坐标,由圆C2:x2+(y-4)2=1可知圆心C2(0,4),写出|MC2|,利用配方法求其最小值,
则|MN|的最小值为|MC2|的最小值减去圆的半径;
(2)设出P,A,B的坐标,再设过点P的圆C2的切线方程为y-x02=k(x-x0),由点到直线的距离公式得到方程(x02-1)k2+2x0(4-x02)k+(x02-4)2-1=0,则其两根为PA,PB的斜率,利用根与系数关系得到其两根和,再把y-x02=k(x-x0)代入y=x2得,x2-kx+kx0-x02=0,结合x0是此方程的根得到x1=k1-x0,x2=k2-x0,然后把AB的中点D的横坐标x用含有x0的代数式表示,再利用单调性结合x0的范围求得AB的中点D的横坐标的取值范围.
则|MN|的最小值为|MC2|的最小值减去圆的半径;
(2)设出P,A,B的坐标,再设过点P的圆C2的切线方程为y-x02=k(x-x0),由点到直线的距离公式得到方程(x02-1)k2+2x0(4-x02)k+(x02-4)2-1=0,则其两根为PA,PB的斜率,利用根与系数关系得到其两根和,再把y-x02=k(x-x0)代入y=x2得,x2-kx+kx0-x02=0,结合x0是此方程的根得到x1=k1-x0,x2=k2-x0,然后把AB的中点D的横坐标x用含有x0的代数式表示,再利用单调性结合x0的范围求得AB的中点D的横坐标的取值范围.
解答:
 解:(1)设M(x,y),由圆C2:x2+(y-4)2=1可知圆心C2(0,4),
解:(1)设M(x,y),由圆C2:x2+(y-4)2=1可知圆心C2(0,4),
则|MC2|=
=
=
=
≥
.
当且仅当M(±
,
)时取“=”,
∴|MN|的最小值为
-1;
(2)设P(x0,x02),A(x1,x12),B(x2,x22),
再设过点P的圆C2的切线方程为y-x02=k(x-x0),①
则
=1,
即(x02-1)k2+2x0(4-x02)k+(x02-4)2-1=0,
设PA,PB的斜率为k1,k2(k1≠k2),则k1,k2是上述方程的两根,
∴k1+k2=
,k1k2=
,
将①代入y=x2得,x2-kx+kx0-x02=0,
由于x0是此方程的根,故x1=k1-x0,x2=k2-x0,
∴AB的中点D的横坐标x=
=
=
=
=
.
∵y=
-x0是[2,4]上的减函数,且2≤x0≤4,
∴y∈[-
,-
],
则x∈[-2,-
].
 解:(1)设M(x,y),由圆C2:x2+(y-4)2=1可知圆心C2(0,4),
解:(1)设M(x,y),由圆C2:x2+(y-4)2=1可知圆心C2(0,4),则|MC2|=
| x2+(y-4)2 |
| x2+(x2-4)2 |
=
| x2+x4-8x2+16 |
(x2-
|
| ||
| 2 |
当且仅当M(±
| ||
| 2 |
| 7 |
| 2 |
∴|MN|的最小值为
| ||
| 2 |
(2)设P(x0,x02),A(x1,x12),B(x2,x22),
再设过点P的圆C2的切线方程为y-x02=k(x-x0),①
则
| |kx0+4-x02| | ||
|
即(x02-1)k2+2x0(4-x02)k+(x02-4)2-1=0,
设PA,PB的斜率为k1,k2(k1≠k2),则k1,k2是上述方程的两根,
∴k1+k2=
| 2x0(x02-4) |
| x02-1 |
| (x02-4)2-1 |
| x02-1 |
将①代入y=x2得,x2-kx+kx0-x02=0,
由于x0是此方程的根,故x1=k1-x0,x2=k2-x0,
∴AB的中点D的横坐标x=
| x1+x2 |
| 2 |
| k1+k2-2x0 |
| 2 |
=
| ||
| 2 |
| 3x0 |
| 1-x02 |
| 3 | ||
|
∵y=
| 1 |
| x0 |
∴y∈[-
| 15 |
| 4 |
| 3 |
| 2 |
则x∈[-2,-
| 4 |
| 5 |
点评:本题主要考查圆与圆锥曲线的综合问题,其中涉及到直线与圆相切的问题,考查了学生的逻辑思维能力和运算能力,是压轴题.

练习册系列答案
相关题目
下列命题中,真命题是( )
| A、?x∈R,x2>0 |
| B、?x0∈R,x02-x0+1=0 |
| C、24是3的倍数且是9的倍数 |
| D、“若b=0,则函数f(x)=ax2+bx+c为偶函数”的逆否命题 |
已知sin(-α)=
,α∈(-
,0),则tanα等于( )
2
| ||
| 3 |
| π |
| 2 |
A、
| ||||
B、-
| ||||
C、2
| ||||
D、-2
|
直线bx-ay+c=0(a>0)是曲线y=ln
在x=3处的切线,f(x)=a•2x+b•3x,若f(x+1)>f(x),则x的取值范围是( )
| 1 |
| x |
| A、(-2,1) |
| B、(1,+∞) |
| C、(-∞,1) |
| D、(-2,-1) |
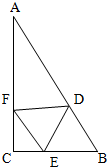 某个公园有个池塘,其形状为直角△ABC,∠C=90°,AB=200米,BC=100米.现在准备新建造一个荷塘,分别在AB,BC,CA上取点D,E,F,建造△DEF连廊(不考虑宽度)供游客休憩,且使△DEF为正三角形,设求△DEF边长的最小值.
某个公园有个池塘,其形状为直角△ABC,∠C=90°,AB=200米,BC=100米.现在准备新建造一个荷塘,分别在AB,BC,CA上取点D,E,F,建造△DEF连廊(不考虑宽度)供游客休憩,且使△DEF为正三角形,设求△DEF边长的最小值.