题目内容
试比较下列各式的大小(不写过程)
(1)1-
与
-
(2)
-
与
-
通过上式请你推测出
-
与
-
(n≥2且n∈N)的大小,并用分析法加以证明.
(1)1-
| 2 |
| 2 |
| 3 |
(2)
| 2 |
| 3 |
| 3 |
| 4 |
通过上式请你推测出
| n-1 |
| n |
| n |
| n+1 |
考点:综合法与分析法(选修),不等式比较大小
专题:证明题,分析法
分析:猜想:
-
<
-
(n≥2且n∈N),再用分析法证明即可.
| n-1 |
| n |
| n |
| n+1 |
解答:
解:(1)1-
<
-
;
(2)
-
<
-
猜想:
-
<
-
(n≥2且n∈N)
证明:要证:
-
<
-
(n≥2且n∈N)
即证:(
-
)2<(
-
)2
整理得:
>
+1
平方整理得:2n-1>2
平方并整理得:1>0而此不等式一定成立,故猜想正确
| 2 |
| 2 |
| 3 |
(2)
| 2 |
| 3 |
| 3 |
| 4 |
猜想:
| n-1 |
| n |
| n |
| n+1 |
证明:要证:
| n-1 |
| n |
| n |
| n+1 |
即证:(
| n-1 |
| n |
| n |
| n+1 |
整理得:
| n2+n |
| n2-n |
平方整理得:2n-1>2
| n2-n |
平方并整理得:1>0而此不等式一定成立,故猜想正确
点评:本题考查归纳猜想,考查分析法的运用,掌握分析法的步骤是关键.

练习册系列答案
相关题目
函数y=
的定义域为( )
| 2-2x |
| A、[0,+∞) |
| B、[1,+∞) |
| C、(-∞,0] |
| D、(-∞,1] |
设a>0,f(x)=ex-
在任一点处的切线的倾斜角的取值范围是[
,
),则a=( )
| a |
| ex |
| π |
| 3 |
| π |
| 2 |
A、
| ||
B、
| ||
| C、3 | ||
D、
|
如果执行如图所示的程序框图,输入x=6,则输出的y值为( )


| A、2 | ||
| B、0 | ||
| C、-1 | ||
D、-
|
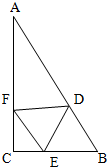 某个公园有个池塘,其形状为直角△ABC,∠C=90°,AB=200米,BC=100米.现在准备新建造一个荷塘,分别在AB,BC,CA上取点D,E,F,建造△DEF连廊(不考虑宽度)供游客休憩,且使△DEF为正三角形,设求△DEF边长的最小值.
某个公园有个池塘,其形状为直角△ABC,∠C=90°,AB=200米,BC=100米.现在准备新建造一个荷塘,分别在AB,BC,CA上取点D,E,F,建造△DEF连廊(不考虑宽度)供游客休憩,且使△DEF为正三角形,设求△DEF边长的最小值.