题目内容
为了了解《中华人民共和国道路交通安全法》在学生中的普及情况,调查部门将某校12名学生分为两组进行问卷调查.第一组的得分情况为:5,6,7,8,9,10;第二组的得分情况为:4,6,7,9,9,10.
(1)根据以上数据,判断两组中哪组更优秀?
(2)把第一组的6名学生的得分看成一个总体.用简单随机抽样方法从这6名学生中抽取2名,他们的得分组成一个样本.求该样本平均数与总体平均数之差的绝对值不超过0.5的概率.
(1)根据以上数据,判断两组中哪组更优秀?
(2)把第一组的6名学生的得分看成一个总体.用简单随机抽样方法从这6名学生中抽取2名,他们的得分组成一个样本.求该样本平均数与总体平均数之差的绝对值不超过0.5的概率.
考点:古典概型及其概率计算公式,众数、中位数、平均数
专题:计算题,概率与统计
分析:(1)求出各组的平均数与方差,比较得到哪组更优秀;
(2)列出所有的基本事件,点点个数求概率.
(2)列出所有的基本事件,点点个数求概率.
解答:
解:(1)第一组的得分平均数为
×(5+6+7+8+9+10)=7.5,
方差为
×[(5-7.5)2+(6-7.5)2+(7-7.5)2+(8-7.5)2+(9-7.5)2+(10-7.5)2]=
×17.5.
第二组的得分平均数为
×(4+6+7+9+9+10)=7.5,
方差为
×[(4-7.5)2+(6-7.5)2+(7-7.5)2+(9-7.5)2+(9-7.5)2+(10-7.5)2]=
×25.5.
说明第一组和第二组的平均得分相同,但是第一组比第二组更稳定,故第一组比第二组更优秀.
(2)简单随机抽样方法从这6名学生中抽取2名,可能的情况有:
(5,6),平均数为5.5;(5,7),平均数为6;(5,8),平均数为6.5;(5,9),平均数为7;
(5,10),平均数为7.5,(6,7),平均数为6.5;(6,8),平均数为7;(6,9),平均数为7.5;
(6,10),平均数为8,(7,8),平均数为7.5,(7,9),平均数为8,(7,10),平均数为8.5,
(8,9),平均数为8.5,(8,10),平均数为9,(9,10),平均数为9.5,
故概率P=
.
| 1 |
| 6 |
方差为
| 1 |
| 6 |
| 1 |
| 6 |
第二组的得分平均数为
| 1 |
| 6 |
方差为
| 1 |
| 6 |
| 1 |
| 6 |
说明第一组和第二组的平均得分相同,但是第一组比第二组更稳定,故第一组比第二组更优秀.
(2)简单随机抽样方法从这6名学生中抽取2名,可能的情况有:
(5,6),平均数为5.5;(5,7),平均数为6;(5,8),平均数为6.5;(5,9),平均数为7;
(5,10),平均数为7.5,(6,7),平均数为6.5;(6,8),平均数为7;(6,9),平均数为7.5;
(6,10),平均数为8,(7,8),平均数为7.5,(7,9),平均数为8,(7,10),平均数为8.5,
(8,9),平均数为8.5,(8,10),平均数为9,(9,10),平均数为9.5,
故概率P=
| 7 |
| 15 |
点评:本题考查了古典概型概率的求法及平均数与方差的求法与应用,属于基础题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
在极坐标系中,已知点A(2,
),B(2,π),点M是圆ρ=2cosθ上任意一点,则点M到直线AB的距离的最小值为( )
| π |
| 2 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
自然数1,2,3,…,n按照一定的顺序排成一个数列:a1,a2,…,an.若满足|a1-1|+|a2-2|+…+|an-n|≤4,则称数列a1,a2,…,an为一个“优数列”.当n=6时,这样的“优数列”共有( )
| A、24个 | B、23个 |
| C、18个 | D、16个 |
函数f(x)=
的最大值是( )
| 2 |
| 1-x(1-x) |
A、
| ||
B、
| ||
C、
| ||
D、
|
规定:若函数f(x)的图象经过某种变换后所得图象对应函数的值域与f(x)的值域相同,则称这种变换是f(x)的T变换,下面给出四个函数及其对应的变换,其中不属于f(x)的T变换的是( )
| A、f(x)=(x-2)2:将函数f(x)的图象关于直线x=3对称 | ||||
| B、f(x)=2x-3-4:将函数f(x)的图象关于x轴对称 | ||||
| C、f(x)=2x-4:将函数f(x)的图象关于直线y=x对称 | ||||
D、f(x)=sin(2+
|
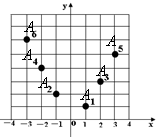 如图,坐标纸上的每个单元格的边长为1,由下往上的六个点:A1,A2,A3,A4,A5,A6的横纵坐标分别对应数列{an}(n∈N*)的前12项,如表所示,按如此规律下去,则a2011+a2012+a2013=
如图,坐标纸上的每个单元格的边长为1,由下往上的六个点:A1,A2,A3,A4,A5,A6的横纵坐标分别对应数列{an}(n∈N*)的前12项,如表所示,按如此规律下去,则a2011+a2012+a2013=