题目内容
设函数f(x)为奇函数,且对任意x,y∈R都有f(x)-f(y)=f(x-y),当x<0时f(x)>0,f(1)=-5,求f(x)在[-2,2]上的最大值.
考点:抽象函数及其应用
专题:函数的性质及应用
分析:根据定义,先确定函数的单调性,不妨令x1<x2,然后根据f(x)-f(y)=f(x-y),当x<0时f(x)>0,可以判断出f(x1)与f(x2)的大小,从而得到单调性,利用赋值法结合f(1)=5,可得f(2)或f(-2)的值,从而确定最值.
解答:
解:设-2≤x1<x2≤2,所以x1-x2<0
由题意得f(x1)-f(x2)=f(x1-x2)>0,
所以f(x1)>f(x2),故该函数在[-2,2]上递减;
所f(x)max=f(-2),
又f(1)=-5,令x=2,y=1得:
f(2)-f(1)=f(2-1)=f(1),
所以f(2)=2f(1)=-10,
所以f(-2)=-f(2)=10,
故f(x)max=10.
由题意得f(x1)-f(x2)=f(x1-x2)>0,
所以f(x1)>f(x2),故该函数在[-2,2]上递减;
所f(x)max=f(-2),
又f(1)=-5,令x=2,y=1得:
f(2)-f(1)=f(2-1)=f(1),
所以f(2)=2f(1)=-10,
所以f(-2)=-f(2)=10,
故f(x)max=10.
点评:本题考查了抽象函数单调性的判断方法,以及函数最值的求法.

练习册系列答案
相关题目
定义域(-1,1)上的函数f(x)满足:f(x)-f(y)=f(
),当x∈(0,1)时,有f(x)<0,若P=f(-
)+f(-
),Q=f(-
),R=f(0),则P,Q,R的大小关系是( )
| x-y |
| 1-xy |
| 1 |
| 5 |
| 1 |
| 11 |
| 1 |
| 2 |
| A、R>Q>P |
| B、Q>P>R |
| C、P>R>Q |
| D、R>P>Q |
S={1,2,…,2003},A是S的三元子集,满足:A中的所有元素可以组成等差数列.那么,这样的三元子集A的个数是( )
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
如图是一个正方体,它的展开图可能是下面四个展开图中的( )


A、 |
B、 |
C、 |
D、 |
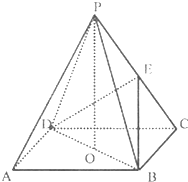 如图,ABCD是正方形,O是正方形的中心,PO⊥底面ABCD,E是PC的中点.
如图,ABCD是正方形,O是正方形的中心,PO⊥底面ABCD,E是PC的中点.