Question

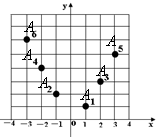如图，坐标纸上的每个单元格的边长为1，由下往上的六个点：A₁，A₂，A₃，A₄，A₅，A₆的横纵坐标分别对应数列{a_n}（n∈N^*）的前12项，如表所示，按如此规律下去，则a₂₀₁₁+a₂₀₁₂+a₂₀₁₃=

 

．

a1	a2	a3	a4	a5	a6	a7	a8	a9	a10	a11	a12
x1	y1	x2	y2	x3	y3	x4	y4	x5	y5	x6	y6

Answer 1

考点：数列的应用

专题：点列、递归数列与数学归纳法

分析：由图形可得六个点A₁，A₂，A₃，A₄，A₅，A₆的坐标，进而得到表格，由表格可得规律a_4n-3=n，a_4n-1=-n．而a₂₀₁₃=a_504×4-3即可得出．

解答： 解：由图形可得：六个点A₁，A₂，A₃，A₄，A₅，A₆的坐标分别为：（1，1），（-1，2），（2，3），（-2，4），（3，5），（-3，6）．
可得：

a1	a2	a3	a4	a5	a6	a7	a8	a9	a10	a11	a12
1	1	-1	2	2	3	-2	4	3	5	-3	6

由表格可知：a₁=1，a₃=-1，a₅=2，a₇=-2，a₉=3，a₁₁=-3．
∴a_4n-3=n，a_4n-1=-n，a_4n=2n．
∴a₂₀₁₁+a₂₀₁₂+a₂₀₁₃
=a_4×503-1+a_4×503+a_4×504-3=-503+1006+504=1007．

点评：本题考查了利用图象和表格找出数列的规律、等差数列的通项公式，考查了观察问题、分析问题和解决问题的能力，是中档题．