题目内容
自然数1，2，3，…，n按照一定的顺序排成一个数列：a1，a2，…，an．若满足|a1-1|+|a2-2|+…+|an-n|≤4，则称数列a1，a2，…，an为一个“优数列”．当n=6时，这样的“优数列”共有（ ）
| A、24个 | B、23个 |
| C、18个 | D、16个 |
考点：排列、组合及简单计数问题
专题：新定义,排列组合
分析：利用新定义，先确定优数列的和只能取0、2、4，再分类讨论，即可得到结论．
解答：
解：由题意，|a1-1|+|a2-2|+…+|an-6|≤4，通过分析可知，当1到6分别对应a1至a6时和，取得最小值0；
任意改变其中两个数ai=i、aj=j的位置，则有|ai-j|+|aj-i|=2|i-j|，
表明一旦改变，和的变化必然是以2为单位，不可能有1、3、5…这样的和出现，
所以，优数列的和只能取0、2、4；
①当和为0时，只有上面提到的1种情况；
②当和为2时，只能是改变相邻位置的两个数而得，否则和2|i-j|必然大于2，共有5种情况；
③当和为4时，需要分类讨论：
（i）改变的是相隔1个数的两个数的情况，也就是i-1和i+1互换位置，有4种情况；
（ii）改变的是三个数轮换的情况，只能是i-1，i，i+1轮换位置，有8种情况；
综上，优数列共有1+5+4+8=18种情况．
故选：C．
任意改变其中两个数ai=i、aj=j的位置，则有|ai-j|+|aj-i|=2|i-j|，
表明一旦改变，和的变化必然是以2为单位，不可能有1、3、5…这样的和出现，
所以，优数列的和只能取0、2、4；
①当和为0时，只有上面提到的1种情况；
②当和为2时，只能是改变相邻位置的两个数而得，否则和2|i-j|必然大于2，共有5种情况；
③当和为4时，需要分类讨论：
（i）改变的是相隔1个数的两个数的情况，也就是i-1和i+1互换位置，有4种情况；
（ii）改变的是三个数轮换的情况，只能是i-1，i，i+1轮换位置，有8种情况；
综上，优数列共有1+5+4+8=18种情况．
故选：C．
点评：本题考查新定义，考查学生分析解决问题的能力，考查分类讨论的数学思想，是中档题．
练习册系列答案
津桥教育计算小状元系列答案
相关题目
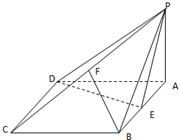如图，四棱锥P-ABCD的底面ABCD是菱形，∠BCD=60°，PA⊥面ABCD，E是AB的中点，F是PC的中点．
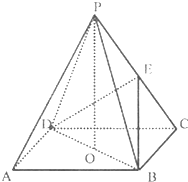如图，ABCD是正方形，O是正方形的中心，PO⊥底面ABCD，E是PC的中点．定义域（-1，1）上的函数f（x）满足：f（x）-f（y）=f（
），当x∈（0，1）时，有f（x）＜0，若P=f（-
）+f（-
），Q=f（-
），R=f（0），则P，Q，R的大小关系是（ ）
| x-y |
| 1-xy |
| 1 |
| 5 |
| 1 |
| 11 |
| 1 |
| 2 |
| A、R＞Q＞P |
| B、Q＞P＞R |
| C、P＞R＞Q |
| D、R＞P＞Q |