题目内容
已知P(2,3)是圆x2+y2=1外一点,PA、PB是过P点的圆的切线,切点为A、B,则直线AB的方程是 .
考点:直线与圆的位置关系
专题:计算题,数形结合
分析:P连接坐标原点O,则OP可求得,OA、OB分别垂直PA、PB,OP与OA的夹角为a,则可求得cosa,进而根据圆心到直线的距离求得圆心到直线的距离d,根据O,P坐标求得OP的斜率,则直线AB的斜率可求,进而设出该直线方程,根据点到直线的距离建立等式求得b,则直线AB的方程可得.
解答:
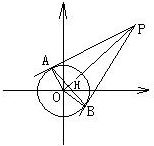 解:如图所示,点P连接坐标原点O,则OP=
解:如图所示,点P连接坐标原点O,则OP=
=
OA、OB分别垂直PA、PB,OP与OA的夹角为a,则cosa=
圆心到直线AB的距离:d=OH=AOcosa=
直线OP的斜率k'=
则直线AB的斜率k=-
,设该直线方程为y=-
x+b,即2x+3y-3b=0
由点到直线距离公式可得圆心(0,0)到直线AB的距离,
即
=d=
,解得b=
或b=-
(舍去)
所以直线AB方程为:2x+3y-1=0
故答案为:2x+3y-1=0.
 解:如图所示,点P连接坐标原点O,则OP=
解:如图所示,点P连接坐标原点O,则OP=| 9+4 |
| 13 |
OA、OB分别垂直PA、PB,OP与OA的夹角为a,则cosa=
| 1 | ||
|
圆心到直线AB的距离:d=OH=AOcosa=
| 1 | ||
|
直线OP的斜率k'=
| 3 |
| 2 |
则直线AB的斜率k=-
| 2 |
| 3 |
| 2 |
| 3 |
由点到直线距离公式可得圆心(0,0)到直线AB的距离,
即
| |0+0-3b| | ||
|
| 1 | ||
|
| 1 |
| 3 |
| 1 |
| 3 |
所以直线AB方程为:2x+3y-1=0
故答案为:2x+3y-1=0.
点评:本题主要考查了直线与圆的位置关系.考查了学生的数形结合的思想和基本的运算能力.

练习册系列答案
 智趣暑假温故知新系列答案
智趣暑假温故知新系列答案 英语小英雄天天默写系列答案
英语小英雄天天默写系列答案
相关题目
实数x,y满足条件
则z=x-y的最大值为( )
|
| A、-1 | B、0 | C、2 | D、4 |
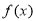 的导函数是
的导函数是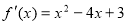 ,则函数
,则函数 (0<a<1)的单调递减区间是( )
(0<a<1)的单调递减区间是( )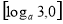 ,
,