题目内容
sin(α-
)+cos(α+
)= .
| π |
| 4 |
| π |
| 4 |
考点:两角和与差的余弦函数,两角和与差的正弦函数
专题:
分析:注意到题中角的互余关系,可化得同一个角的三角函数形式,进而发现其值是0.
解答:
解:∵(α+
)-(α-
)=
,
∴sin(α-
)+cos(α+
)=sin(α-
)+cos[
+(α-
)]
=sin(α-
)-sin(α-
)=0.
故填:0.
| π |
| 4 |
| π |
| 4 |
| π |
| 2 |
∴sin(α-
| π |
| 4 |
| π |
| 4 |
| π |
| 4 |
| π |
| 2 |
| π |
| 4 |
=sin(α-
| π |
| 4 |
| π |
| 4 |
故填:0.
点评:关于角变换此类问题不宜对已知角的三角函数用和(差)角公式展开,应充分利用角间的关系,灵活处理,沟通条件与结论中的角的差异.

练习册系列答案
相关题目
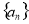 中,
中, 且
且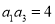 ,
, 是
是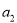 和
和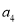 的等差中项.
的等差中项.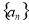 的通项公式;
的通项公式;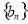 满足
满足 ,(
,( ),求数列
),求数列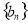 的前
的前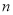 项和
项和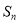 .
. 满足
满足 .
. ,求证:数列
,求证:数列 是等比数列并求其通项公式;
是等比数列并求其通项公式; +
+ + +
+ +
 .
. 的极坐标方程为
的极坐标方程为 ,以极点为坐标原点,极轴为
,以极点为坐标原点,极轴为 轴正半轴建立
轴正半轴建立 的参数方程为
的参数方程为 (
( 为参数)
为参数) 的极坐标方程化为直角坐标方程,把直线
的极坐标方程化为直角坐标方程,把直线 的参数方程化为普通方程;
的参数方程化为普通方程; 被曲线
被曲线 截得的线段
截得的线段 的长.
的长.