题目内容
设tan
=t.
(1)求证:
=
(t+1);
(2)当tan(
+2θ)=
时,利用以上结果求
的值.
| θ |
| 2 |
(1)求证:
| 1+sinθ |
| 1+sinθ+cosθ |
| 1 |
| 2 |
(2)当tan(
| π |
| 2 |
| 3 |
| 4 |
| 1-sin4θ |
| 1-sin4θ-cos4θ |
考点:三角函数的恒等变换及化简求值
专题:综合题
分析:(1)利用万能公式用tan
分别表示出sinθ和cosθ,代入整理可证明原式.
(2)利用诱导公式和(1)中的结论,整理成tan(
+2θ)的形式,最后代入即可.
| θ |
| 2 |
(2)利用诱导公式和(1)中的结论,整理成tan(
| π |
| 2 |
解答:
解:(1)证明:由sinθ=
及cosθ=
得1+sinθ=
=
,1+sinθ+cosθ=
=
故
=
(t+1).
(2)解:由(1)及tan(
+2θ)=
得
=
=
[tan(
+2θ)+1]=
.
2tan
| ||
1+tan2
|
1-tan2
| ||
1+tan2
|
得1+sinθ=
(1+tan
| ||
1+tan2
|
| (1+t)2 |
| 1+t2 |
2(1+tan
| ||
1+tan2
|
| 2(1+t) |
| 1+t2 |
故
| 1+sinθ |
| 1+sinθ+cosθ |
| 1 |
| 2 |
(2)解:由(1)及tan(
| π |
| 2 |
| 3 |
| 4 |
| 1-sin4θ |
| 1-sin4θ-cos4θ |
| 1+sin(π+4θ) |
| 1+sin(π+4θ)+cos(π+4θ) |
| 1 |
| 2 |
| π |
| 2 |
| 7 |
| 8 |
点评:本题主要考查了三角函数恒等变换及化简求值.考查了学生对公式的正用,逆用和变形用.

练习册系列答案
相关题目
等差数列{an}的首项a1=-5,它的前11项的平均值为5,从前11项中抽去某一项后,余下的10项平均值为4,则抽去的一项是( )
| A、a5 |
| B、a6 |
| C、a10 |
| D、a11 |
 如图是某电视剧在各年龄段人群收视情况的频率分布直方图.若某村观看此电视剧的观众人数为1400人,则其中50岁以上(含50岁)的观众约有( )人.
如图是某电视剧在各年龄段人群收视情况的频率分布直方图.若某村观看此电视剧的观众人数为1400人,则其中50岁以上(含50岁)的观众约有( )人.| A、504 | B、501 |
| C、500 | D、550 |
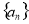 中,
中, 且
且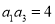 ,
, 是
是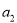 和
和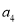 的等差中项.
的等差中项.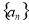 的通项公式;
的通项公式;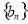 满足
满足 ,(
,( ),求数列
),求数列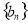 的前
的前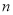 项和
项和 .
.