题目内容
已知f(x)=x2+2(a-1)x+2在(-∞,-4)上是减函数,且f(x)>0,求a的取值范围.
考点:二次函数的性质,函数单调性的性质
专题:计算题
分析:要让f(x)=x2+2(a-1)x+2在(-∞,-4)上是减函数,所以需要对称轴方程位于区间的右侧,结合单调性又有f(-4)≥0,解不等式组可得答案.
解答:
解:因为f(x)=x2+2(a-1)x+2为开口向上的二次函数,
其对称轴为x=1-a,
故须有1-a≥-4且f(-4)≥0,
即为1-a≥-4且(-4)2+2(a-1)(-4)+2≥0
解得a≤3,
所以a的取值范围为a≤3.
其对称轴为x=1-a,
故须有1-a≥-4且f(-4)≥0,
即为1-a≥-4且(-4)2+2(a-1)(-4)+2≥0
解得a≤3,
所以a的取值范围为a≤3.
点评:函数的单调区间和函数在某个区间上单调不是同一个概念,应该分清对待.

练习册系列答案
相关题目
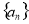 中,
中, 且
且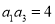 ,
, 是
是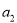 和
和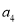 的等差中项.
的等差中项.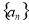 的通项公式;
的通项公式;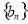 满足
满足 ,(
,( ),求数列
),求数列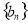 的前
的前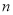 项和
项和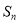 .
.
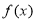 的最小正周期
的最小正周期 中,
中,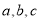 分别是
分别是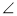 A、
A、 B、
B、 ,
, ,
,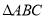 的面积为
的面积为 ,求
,求 的值
的值