题目内容
过点A(1,1)与曲线C:y=x3相切的直线方程是 .
考点:利用导数研究曲线上某点切线方程
专题:计算题
分析:设切点为(x0,y0),则y0=x03,由于直线l经过点(1,1),可得切线的斜率,再根据导数的几何意义求出曲线在点x0处的切线斜率,便可建立关于x0的方程.从而可求方程.
解答:
解:若直线与曲线切于点(x0,y0)(x0≠0),则k=
=
=
+x0+1
.∵y′=3x2,∴y′|x=x0=3x02,∴2x02-x0-1=0,∴x0=1,x0=-
,
∴过点A(1,1)与曲线C:y=x3相切的直线方程为3x-y-2=0或3x-4y+1=0,
故答案为3x-y-2=0或3x-4y+1=0
| y0-1 |
| x0-1 |
| ||
| x0-1 |
| x | 2 0 |
.∵y′=3x2,∴y′|x=x0=3x02,∴2x02-x0-1=0,∴x0=1,x0=-
| 1 |
| 2 |
∴过点A(1,1)与曲线C:y=x3相切的直线方程为3x-y-2=0或3x-4y+1=0,
故答案为3x-y-2=0或3x-4y+1=0
点评:此题考查学生会利用导数求曲线上过某点切线方程的斜率,会根据一点坐标和斜率写出直线的方程,是一道综合题.

练习册系列答案
 永乾教育寒假作业快乐假期延边人民出版社系列答案
永乾教育寒假作业快乐假期延边人民出版社系列答案
相关题目
等差数列{an}的首项a1=-5,它的前11项的平均值为5,从前11项中抽去某一项后,余下的10项平均值为4,则抽去的一项是( )
| A、a5 |
| B、a6 |
| C、a10 |
| D、a11 |
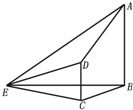 如图,在四棱锥E-ABCD中,AB⊥平面BCE,CD⊥平面BCE,AB=BC=CE=2CD=2,∠BCE=120°.
如图,在四棱锥E-ABCD中,AB⊥平面BCE,CD⊥平面BCE,AB=BC=CE=2CD=2,∠BCE=120°.