题目内容

13．已知{an}为等差数列，若a1+a5+a9=8π，则cos（a2+a8）=（　　）
A．$-\frac{1}{2}$B．$-\frac{{\sqrt{3}}}{2}$C．$\frac{1}{2}$D．$\frac{{\sqrt{3}}}{2}$

分析 利用等差数列的性质可得a1+a9=a2+a8=2a5，结合已知，可求出a5，进而求出cos（a2+a8）．

解答 解：∵{an}为等差数列，
∴a1+a9=a2+a8=2a5，
∵a1+a5+a9=8π，
∴a5=$\frac{8π}{3}$，a2+a8=$\frac{16π}{3}$，
∴cos（a2+a8）=cos$\frac{16π}{3}$=$-\frac{1}{2}$．
故选：A．

点评 本题应用了等差数列的性质：{an}为等差数列，当m+n=p+q（m，n，p，q∈N+）时，am+an=ap+aq．
特例：若m+n=2p（m，n，p∈N+），则am+an=2ap．

练习册系列答案
相关题目
3．复数z满足（1-i）z=m+i （m∈R，i为虚数单位），在复平面上z对应的点不可能在    （　　）
A．第一象限B．第二象限C．第三象限D．第四象限
4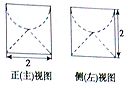．若某圆柱体的上部挖掉一个半球，下部挖掉一个圆锥后所得的几何体的三视图中的正（主）视图和侧（左）视图如图所示，则此时几何体的体积是（　　）
A．2πB．$\frac{4π}{3}$C．πD．$\frac{π}{2}$
1．数列{an}满足a1=1，${a_{n+1}}=\frac{{{2^{n+1}}{a_n}}}{{{a_n}+{2^n}}}$（n∈N+）．
（1）证明：数列$\left\{{\frac{2^n}{a_n}}\right\}$是等差数列；
（2）求数列{an}的通项公式an．
8．若变量x，y满足约束条件$\left\{\begin{array}{l}x+y-3≤0\\ x-y+1＞0\\ y≥1\end{array}$，则z=$\frac{x+2y}{x}$的最小值为（　　）
A．0B．1C．2D．3
18．用平行于圆锥底面的截面去截圆锥，所得小圆锥的侧面积与原来大圆锥的侧面积的比是$\frac{1}{2}$，则小圆锥的高与大圆锥的高的比是（　　）
A．$\frac{1}{2}$B．1C．$\frac{\sqrt{2}}{2}$D．$\sqrt{2}$
5．某几何体的三视图如图所示，这几何体为（　　）
A．长方体B．圆柱C．圆台D．棱柱
2．在△ABC中，a、b、c分别是∠A、∠B、∠C的对边，已知c=$\sqrt{3}$，b=1，B=30°．求角C及△ABC的面积S．
3．已知a，b，c是锐角△ABC中的角A、B、C的对边，若$B=\frac{π}{4}$，则$\frac{acosC-ccosA}{b}$的取值范围为（　　）
A．（-1，1）B．$（-\frac{1}{2}，\frac{1}{2}）$C．$（-\sqrt{2}，\sqrt{2}）$D．$（-\frac{{\sqrt{2}}}{2}，\frac{{\sqrt{2}}}{2}）$

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网