题目内容
5．某几何体的三视图如图所示，这几何体为（ ）
| A． | 长方体 | B． | 圆柱 | C． | 圆台 | D． | 棱柱 |
分析 由三视图可知几何体的现状．
解答 解：由三视图可知，几何体为四棱柱，
故选D．
点评 本题考查三视图，考查直观图，比较基础．
练习册系列答案
相关题目
15．已知f（x）=$\left\{\begin{array}{l}{x^2}-2ax，x≥2\\ 4x-6，x＜2\end{array}$在定义域R上是增函数，则a的取值范围是（ ）
| A． | a≥0 | B． | a≤0 | C． | $a≤\frac{1}{2}$ | D． | a≤-1 |
13．已知{an}为等差数列，若a1+a5+a9=8π，则cos（a2+a8）=（ ）
| A． | $-\frac{1}{2}$ | B． | $-\frac{{\sqrt{3}}}{2}$ | C． | $\frac{1}{2}$ | D． | $\frac{{\sqrt{3}}}{2}$ |
20．已知点 A（1，3），B（3，1），C（-1，0），则△ABC的面积为（ ）
| A． | 5 | B． | $5\sqrt{2}$ | C． | 10 | D． | $10\sqrt{2}$ |
10．某同学用“五点法”画函数f（x）=Asin（ωx+φ）（ω＞0，|φ|＜$\frac{π}{2}$）在某一个周期内的图象时，列表并填入了部分数据，如表：
（1）请将如表数据补充完整，并直接写出函数f（x）的解析式；
（2）将y=f（x）图象上所有点向左平行移动$\frac{π}{3}$个单位长度，得到y=g（x）的图象，求y=g（x）的图象离原点O最近的对称中心．
| ωx+φ | 0 | $\frac{π}{2}$ | π | $\frac{3π}{2}$ | 2π |
| x | $\frac{π}{2}$ | $\frac{3π}{2}$ | $\frac{5π}{2}$ | $\frac{7π}{2}$ | $\frac{9π}{2}$ |
| Asin（ωx+φ） | 0 | 3 | 0 | -3 | 0 |
（2）将y=f（x）图象上所有点向左平行移动$\frac{π}{3}$个单位长度，得到y=g（x）的图象，求y=g（x）的图象离原点O最近的对称中心．
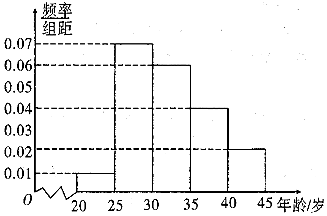“一带一路”是“丝绸之路经济带”和“21世纪海上丝绸之路”的简称，某市为了了解人们对“一带一路”的认知程度，对不同年龄和不同职业的人举办了一次“一带一路”知识竞赛，满分100分（90分及以上为认知程度高），现从参赛者中抽取了x人，按年龄分成5组（第一组：[20，25），第二组：[25，30），第三组：[30，35），第四组：[35，40），第五组：[40，45]），得到如图所示的频率分布直方图，已知第一组有6人．