题目内容
4．
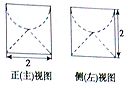若某圆柱体的上部挖掉一个半球，下部挖掉一个圆锥后所得的几何体的三视图中的正（主）视图和侧（左）视图如图所示，则此时几何体的体积是（ ）| A． | 2π | B． | $\frac{4π}{3}$ | C． | π | D． | $\frac{π}{2}$ |
分析 由正视图与侧视图可知：圆柱的底面直径为2，高为2，球的直径为2，圆锥的底面直径为2，高为1．即可得出结论．
解答 解：由正视图与侧视图可知：圆柱的底面直径为2，高为2，球的直径为2，圆锥的底面直径为2，高为1．
可得该几何体的体积V=π×12×2-$\frac{1}{2}×\frac{4}{3}π•{1}^{3}$-$\frac{1}{3}×π×{1}^{2}×1$=π．
故选C．
点评 本题考查了圆柱、圆锥、球的三视图、体积计算公式，考查了推理能力与计算能力，属于中档题．
练习册系列答案
同步练习强化拓展系列答案
相关题目
14．已知复数z在复平面内对应的点为（-1，1），则复数$\frac{z+3}{z+2}$的模为（ ）
| A． | $\sqrt{10}$ | B． | $\frac{\sqrt{10}}{2}$ | C． | $\sqrt{2}$ | D． | 2 |
15．已知f（x）=$\left\{\begin{array}{l}{x^2}-2ax，x≥2\\ 4x-6，x＜2\end{array}$在定义域R上是增函数，则a的取值范围是（ ）
| A． | a≥0 | B． | a≤0 | C． | $a≤\frac{1}{2}$ | D． | a≤-1 |
19．设锐角△ABC的三个内角A，B，C的对边分别为a，b，c成等比数列，且sinAsinC=$\frac{3}{4}$，则角B=（ ）
| A． | $\frac{π}{6}$ | B． | $\frac{π}{3}$ | C． | $\frac{π}{4}$ | D． | $\frac{2π}{3}$ |
9．要得到函数f（x）=sin2x+$\sqrt{3}$cos2x的图象，可将y=2sin2x的图象向左平移多少个单位（ ）
| A． | $\frac{π}{6}$个 | B． | $\frac{π}{3}$个 | C． | $\frac{π}{4}$个 | D． | $\frac{π}{12}$个 |
13．已知{an}为等差数列，若a1+a5+a9=8π，则cos（a2+a8）=（ ）
| A． | $-\frac{1}{2}$ | B． | $-\frac{{\sqrt{3}}}{2}$ | C． | $\frac{1}{2}$ | D． | $\frac{{\sqrt{3}}}{2}$ |