题目内容
3.复数z满足(1-i)z=m+i (m∈R,i为虚数单位),在复平面上z对应的点不可能在 ( )| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
分析 由(1-i)z=m+i,得$z=\frac{m+i}{1-i}$,再利用复数代数形式的乘除运算化简复数z,令复数的实部大于0,虚部小于0,得到不等式无解,即对应的点不在第四象限.
解答 解:由(1-i)z=m+i,
得$z=\frac{m+i}{1-i}$=$\frac{(m+i)(1+i)}{(1-i)(1+i)}=\frac{(m-1)+(m+1)i}{2}$=$\frac{m-1}{2}+\frac{m+1}{2}i$,
当m-1>0且m+1>0时,有解:m>1;
当m-1<0且m+1>0时,有解:-1<m<1;
当m-1<0且m+1<0时,有解:m<-1;
当m-1>0且m+1<0时,无解.
故选:D.
点评 本题考查了复数代数形式的乘除运算,考查了复数的代数表示法及其几何意义,是基础题.

练习册系列答案
 中考利剑中考试卷汇编系列答案
中考利剑中考试卷汇编系列答案 教育世家状元卷系列答案
教育世家状元卷系列答案 黄冈课堂作业本系列答案
黄冈课堂作业本系列答案
相关题目
14.已知复数z在复平面内对应的点为(-1,1),则复数$\frac{z+3}{z+2}$的模为( )
| A. | $\sqrt{10}$ | B. | $\frac{\sqrt{10}}{2}$ | C. | $\sqrt{2}$ | D. | 2 |
11.在△ABC中,三个内角A,B,C的对边分别为a,b,c,若△ABC的面积为S,且4S=(a+b)2-c2,则sin($\frac{π}{4}$+C)等于( )
| A. | 1 | B. | -$\frac{\sqrt{2}}{2}$ | C. | $\frac{\sqrt{2}}{2}$ | D. | $\frac{\sqrt{3}}{2}$ |
8.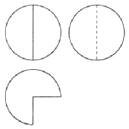 如图,某几何体的三视图由半径相同的圆和扇形构成,若府视图中扇形的面积为3π,則该几何体的体积等于( )
如图,某几何体的三视图由半径相同的圆和扇形构成,若府视图中扇形的面积为3π,則该几何体的体积等于( )
 如图,某几何体的三视图由半径相同的圆和扇形构成,若府视图中扇形的面积为3π,則该几何体的体积等于( )
如图,某几何体的三视图由半径相同的圆和扇形构成,若府视图中扇形的面积为3π,則该几何体的体积等于( )| A. | 8π | B. | $\frac{16π}{3}$ | C. | 4π | D. | $\frac{4π}{3}$ |
15.已知f(x)=$\left\{\begin{array}{l}{x^2}-2ax,x≥2\\ 4x-6,x<2\end{array}$在定义域R上是增函数,则a的取值范围是( )
| A. | a≥0 | B. | a≤0 | C. | $a≤\frac{1}{2}$ | D. | a≤-1 |
13.已知{an}为等差数列,若a1+a5+a9=8π,则cos(a2+a8)=( )
| A. | $-\frac{1}{2}$ | B. | $-\frac{{\sqrt{3}}}{2}$ | C. | $\frac{1}{2}$ | D. | $\frac{{\sqrt{3}}}{2}$ |