题目内容
18．用平行于圆锥底面的截面去截圆锥，所得小圆锥的侧面积与原来大圆锥的侧面积的比是$\frac{1}{2}$，则小圆锥的高与大圆锥的高的比是（ ）| A． | $\frac{1}{2}$ | B． | 1 | C． | $\frac{\sqrt{2}}{2}$ | D． | $\sqrt{2}$ |
分析 设小圆锥的半径为r，大圆锥的半径为R；母线长分别为l，L；高分别为h，H．由于用平行于圆锥底面的截面去截圆锥，可得$\frac{r}{R}=\frac{l}{L}=\frac{h}{H}$．利用圆锥侧面积计算公式即可得出．
解答 解：设小圆锥的半径为r，大圆锥的半径为R；
母线长分别为l，L；高分别为h，H．
∵用平行于圆锥底面的截面去截圆锥，
则$\frac{r}{R}=\frac{l}{L}=\frac{h}{H}$．
由小圆锥的侧面积与原来大圆锥的侧面积的比是$\frac{1}{2}$，
则$\frac{\frac{1}{2}•2πr•l}{\frac{1}{2}•2πR•L}$=$\frac{1}{2}$，∴$\frac{{h}^{2}}{{H}^{2}}=\frac{1}{2}$．
∴$\frac{h}{H}$=$\frac{\sqrt{2}}{2}$．
故选：C．
点评 本题考查了圆锥侧面积计算公式、相似三角形的性质，考查了推理能力与计算能力，属于中档题．
练习册系列答案
阅读快车系列答案
相关题目
8．
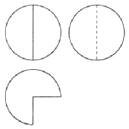如图，某几何体的三视图由半径相同的圆和扇形构成，若府视图中扇形的面积为3π，則该几何体的体积等于（ ）
如图，某几何体的三视图由半径相同的圆和扇形构成，若府视图中扇形的面积为3π，則该几何体的体积等于（ ）| A． | 8π | B． | $\frac{16π}{3}$ | C． | 4π | D． | $\frac{4π}{3}$ |
9．要得到函数f（x）=sin2x+$\sqrt{3}$cos2x的图象，可将y=2sin2x的图象向左平移多少个单位（ ）
| A． | $\frac{π}{6}$个 | B． | $\frac{π}{3}$个 | C． | $\frac{π}{4}$个 | D． | $\frac{π}{12}$个 |
13．已知{an}为等差数列，若a1+a5+a9=8π，则cos（a2+a8）=（ ）
| A． | $-\frac{1}{2}$ | B． | $-\frac{{\sqrt{3}}}{2}$ | C． | $\frac{1}{2}$ | D． | $\frac{{\sqrt{3}}}{2}$ |
3．已知集合A={1，2，3}，B={2，m，4}，A∩B={2，3}，则m=（ ）
| A． | 3 | B． | 1 | C． | 2 | D． | 4 |
10．某同学用“五点法”画函数f（x）=Asin（ωx+φ）（ω＞0，|φ|＜$\frac{π}{2}$）在某一个周期内的图象时，列表并填入了部分数据，如表：
（1）请将如表数据补充完整，并直接写出函数f（x）的解析式；
（2）将y=f（x）图象上所有点向左平行移动$\frac{π}{3}$个单位长度，得到y=g（x）的图象，求y=g（x）的图象离原点O最近的对称中心．
| ωx+φ | 0 | $\frac{π}{2}$ | π | $\frac{3π}{2}$ | 2π |
| x | $\frac{π}{2}$ | $\frac{3π}{2}$ | $\frac{5π}{2}$ | $\frac{7π}{2}$ | $\frac{9π}{2}$ |
| Asin（ωx+φ） | 0 | 3 | 0 | -3 | 0 |
（2）将y=f（x）图象上所有点向左平行移动$\frac{π}{3}$个单位长度，得到y=g（x）的图象，求y=g（x）的图象离原点O最近的对称中心．
7．在△ABC中，已知sin（A+B）=$\frac{1}{2}$，则∠C是（ ）
| A． | 150° | B． | 30°或150° | C． | 60° | D． | 60°或120° |