题目内容
2.在△ABC中,a、b、c分别是∠A、∠B、∠C的对边,已知c=$\sqrt{3}$,b=1,B=30°.求角C及△ABC的面积S.分析 由已知利用正弦定理可求sinC的值,结合C的范围,分类讨论,利用三角形内角和定理可求A的值,进而利用三角形面积公式即可计算得解.
解答 (本题满分为13分)
解:∵$\frac{sinC}{sinB}=\frac{c}{b}$,$sinC=\frac{{\sqrt{3}}}{2}$,…(3分)
∵c>b,
∴C=60°或C=120°,…(6分)
(Ⅰ)C=60°时,A=180°-300-600=900,
∴${S_{△ABC}}=\frac{1}{2}bc=\frac{1}{2}×1×\sqrt{3}=\frac{{\sqrt{3}}}{2}$.…(9分)
(Ⅱ)C=120°时,A=180°-300-1200=300,
∴${S_{△ABC}}=\frac{1}{2}bcsinA=\frac{1}{2}×1×\sqrt{3}×\frac{1}{2}=\frac{{\sqrt{3}}}{4}$,
∴所求的C=60°,${S_{△ABC}}=\frac{{\sqrt{3}}}{2}$或C=120°,${S_{△ABC}}=\frac{{\sqrt{3}}}{4}$.…(13分)
点评 本题主要考查了正弦定理,三角形内角和定理,三角形面积公式在解三角形中的应用,考查了分类讨论思想和转化思想,属于基础题.

练习册系列答案
 普通高中同步练习册系列答案
普通高中同步练习册系列答案 优翼小帮手同步口算系列答案
优翼小帮手同步口算系列答案
相关题目
13.已知{an}为等差数列,若a1+a5+a9=8π,则cos(a2+a8)=( )
| A. | $-\frac{1}{2}$ | B. | $-\frac{{\sqrt{3}}}{2}$ | C. | $\frac{1}{2}$ | D. | $\frac{{\sqrt{3}}}{2}$ |
10.某同学用“五点法”画函数f(x)=Asin(ωx+φ)(ω>0,|φ|<$\frac{π}{2}$)在某一个周期内的图象时,列表并填入了部分数据,如表:
(1)请将如表数据补充完整,并直接写出函数f(x)的解析式;
(2)将y=f(x)图象上所有点向左平行移动$\frac{π}{3}$个单位长度,得到y=g(x)的图象,求y=g(x)的图象离原点O最近的对称中心.
| ωx+φ | 0 | $\frac{π}{2}$ | π | $\frac{3π}{2}$ | 2π |
| x | $\frac{π}{2}$ | $\frac{3π}{2}$ | $\frac{5π}{2}$ | $\frac{7π}{2}$ | $\frac{9π}{2}$ |
| Asin(ωx+φ) | 0 | 3 | 0 | -3 | 0 |
(2)将y=f(x)图象上所有点向左平行移动$\frac{π}{3}$个单位长度,得到y=g(x)的图象,求y=g(x)的图象离原点O最近的对称中心.
7.在△ABC中,已知sin(A+B)=$\frac{1}{2}$,则∠C是( )
| A. | 150° | B. | 30°或150° | C. | 60° | D. | 60°或120° |
11. 某校高三期中考试后,数学教师对本次全部数学成绩按1:20进行分层抽样,随机抽取了20名学生的成绩为样本,成绩用茎叶图记录如图所示,但部分数据不小心丢失,同时得到如表所示的频率分布表:
某校高三期中考试后,数学教师对本次全部数学成绩按1:20进行分层抽样,随机抽取了20名学生的成绩为样本,成绩用茎叶图记录如图所示,但部分数据不小心丢失,同时得到如表所示的频率分布表:
(Ⅰ)求表中a,b,c的值,并估计这次考试全校高三数学成绩的及格率(成绩在[90,150]内为及格);
(Ⅱ)设茎叶图中成绩在[100,120)范围内的样本的中位数为m,若从成绩在[100,120)范围内的样品中每次随机抽取1个,每次取出不放回,连续取两次,求取出两个样本中恰好一个是数字m的概率.
 某校高三期中考试后,数学教师对本次全部数学成绩按1:20进行分层抽样,随机抽取了20名学生的成绩为样本,成绩用茎叶图记录如图所示,但部分数据不小心丢失,同时得到如表所示的频率分布表:
某校高三期中考试后,数学教师对本次全部数学成绩按1:20进行分层抽样,随机抽取了20名学生的成绩为样本,成绩用茎叶图记录如图所示,但部分数据不小心丢失,同时得到如表所示的频率分布表:| 分数段 | [50,70) | [70,90) | [90,110) | [110,130) | [130,150] | 总计 |
| 频数 | c | b | ||||
| 频率 | a |
(Ⅱ)设茎叶图中成绩在[100,120)范围内的样本的中位数为m,若从成绩在[100,120)范围内的样品中每次随机抽取1个,每次取出不放回,连续取两次,求取出两个样本中恰好一个是数字m的概率.
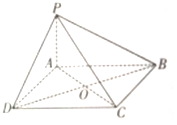 如图所示,四棱锥P-ABCD中,底面ABCD为平行四边形,PA⊥AD,PA⊥AB,AB=AD,AC与BD交于点O.
如图所示,四棱锥P-ABCD中,底面ABCD为平行四边形,PA⊥AD,PA⊥AB,AB=AD,AC与BD交于点O.