题目内容
3．已知a，b，c是锐角△ABC中的角A、B、C的对边，若$B=\frac{π}{4}$，则$\frac{acosC-ccosA}{b}$的取值范围为（ ）| A． | （-1，1） | B． | $（-\frac{1}{2}，\frac{1}{2}）$ | C． | $（-\sqrt{2}，\sqrt{2}）$ | D． | $（-\frac{{\sqrt{2}}}{2}，\frac{{\sqrt{2}}}{2}）$ |
分析 由正弦定理、和差公式、同角三角函数基本关系式可得：$\frac{acosC-ccosA}{b}$=$\frac{sinAcosC-sinCcosA}{sinB}$=$\frac{\frac{tanA}{tanC}-1}{\frac{tanA}{tanC}+1}$，由锐角△ABC，可得$\frac{tanA}{tanC}$=t＞0，再利用函数的单调性即可得出．
解答 解：由正弦定理可得：$\frac{acosC-ccosA}{b}$=$\frac{sinAcosC-sinCcosA}{sinB}$=$\frac{sinAcosC-cosAsinC}{sinAcosC+cosAsinC}$=$\frac{tanA-tanC}{tanA+tanC}$=$\frac{\frac{tanA}{tanC}-1}{\frac{tanA}{tanC}+1}$，
∵锐角△ABC，∴$\frac{tanA}{tanC}$=t＞0，
∴$\frac{acosC-ccosA}{b}$=$\frac{t-1}{t+1}$=1-$\frac{2}{t+1}$∈（-1，1），
故选：A．
点评 本题考查了正弦定理、和差公式、同角三角函数基本关系式、函数的单调性，考查了推理能力与计算能力，属于中档题．
练习册系列答案
相关题目
13．已知{an}为等差数列，若a1+a5+a9=8π，则cos（a2+a8）=（ ）
| A． | $-\frac{1}{2}$ | B． | $-\frac{{\sqrt{3}}}{2}$ | C． | $\frac{1}{2}$ | D． | $\frac{{\sqrt{3}}}{2}$ |
11．
某校高三期中考试后，数学教师对本次全部数学成绩按1：20进行分层抽样，随机抽取了20名学生的成绩为样本，成绩用茎叶图记录如图所示，但部分数据不小心丢失，同时得到如表所示的频率分布表：
（Ⅰ）求表中a，b，c的值，并估计这次考试全校高三数学成绩的及格率（成绩在[90，150]内为及格）；
（Ⅱ）设茎叶图中成绩在[100，120）范围内的样本的中位数为m，若从成绩在[100，120）范围内的样品中每次随机抽取1个，每次取出不放回，连续取两次，求取出两个样本中恰好一个是数字m的概率．
某校高三期中考试后，数学教师对本次全部数学成绩按1：20进行分层抽样，随机抽取了20名学生的成绩为样本，成绩用茎叶图记录如图所示，但部分数据不小心丢失，同时得到如表所示的频率分布表：| 分数段 | [50，70） | [70，90） | [90，110） | [110，130） | [130，150] | 总计 |
| 频数 | c | b | ||||
| 频率 | a |
（Ⅱ）设茎叶图中成绩在[100，120）范围内的样本的中位数为m，若从成绩在[100，120）范围内的样品中每次随机抽取1个，每次取出不放回，连续取两次，求取出两个样本中恰好一个是数字m的概率．
18．若$α∈（\frac{π}{2}，π）$，则$\frac{3}{2}cos2α=sin（\frac{π}{4}-α）$，则sin2α的值为（ ）
| A． | $\frac{2}{9}$ | B． | $-\frac{2}{9}$ | C． | $\frac{7}{9}$ | D． | $-\frac{7}{9}$ |
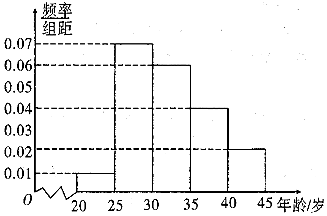“一带一路”是“丝绸之路经济带”和“21世纪海上丝绸之路”的简称，某市为了了解人们对“一带一路”的认知程度，对不同年龄和不同职业的人举办了一次“一带一路”知识竞赛，满分100分（90分及以上为认知程度高），现从参赛者中抽取了x人，按年龄分成5组（第一组：[20，25），第二组：[25，30），第三组：[30，35），第四组：[35，40），第五组：[40，45]），得到如图所示的频率分布直方图，已知第一组有6人．
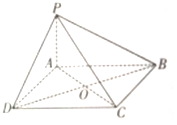如图所示，四棱锥P-ABCD中，底面ABCD为平行四边形，PA⊥AD，PA⊥AB，AB=AD，AC与BD交于点O．