题目内容
某地西红柿从2月1号起开始上市,通过市场调查,得到西红柿种植成本Q(单位:元/100kg)与上市时间t(距2月1日的天数,单位:天)的部分数据如下表:
(Ⅰ)根据上表数据,从下列函数Q=at+b,Q=at2+bt+c,Q=a•bt,Q=a•logbt中选取一个函数描述西红柿种植成本Q与上市时间t的变化关系,说明选择理由,并求所选函数的解析式;
(Ⅱ)利用你选取的函数,求西红柿种植成本Q最低时的上市天数及最低种植成本.
| 时间t | 50 | 110 | 250 |
| 成本Q | 150 | 108 | 150 |
(Ⅱ)利用你选取的函数,求西红柿种植成本Q最低时的上市天数及最低种植成本.
考点:塞瓦定理,函数模型的选择与应用
专题:计算题,函数的性质及应用
分析:(Ⅰ)由提供的数据知,描述西红柿种植成本Q与上市时间t的变化关系函数不可能是单调函数,故选取二次函数Q=at2+bt+c进行描述,将表格所提供的三组数据(50,150),(110,108),(250,150)代入Q,即得函数解析式;
(Ⅱ)由二次函数的图象与性质可得,函数Q在t取何值时,有最小值.
(Ⅱ)由二次函数的图象与性质可得,函数Q在t取何值时,有最小值.
解答:
解:(Ⅰ)根据表中数据,表述西红柿种植成本Q与上市时间t的变化关系的函数不是单调函数,这与函数Q=at+b,Q=a•bt,Q=a•logbt均具有单调性不符,所以,在a≠0的前提下,可选取二次函数Q=at2+bt+c进行描述. …4分
把表格提供的三对数据代入该解析式得到:
…6分
解得a=
,b=-
,c=
. …9分
所以,西红柿种植成本Q与上市时间t的函数关系是Q=
t2-
t+
.…10分
(Ⅱ)当t=-=150天时,西红柿种植成本Q最低为Q=
×1502-
×150+
=100(元/100kg). …12分
所以,西红柿种植成本Q最低时的上市天数是150天,最低种植成本为100(元/100kg) …13分.
把表格提供的三对数据代入该解析式得到:
|
解得a=
| 1 |
| 200 |
| 3 |
| 2 |
| 425 |
| 2 |
所以,西红柿种植成本Q与上市时间t的函数关系是Q=
| 1 |
| 200 |
| 3 |
| 2 |
| 425 |
| 2 |
(Ⅱ)当t=-=150天时,西红柿种植成本Q最低为Q=
| 1 |
| 200 |
| 3 |
| 2 |
| 425 |
| 2 |
所以,西红柿种植成本Q最低时的上市天数是150天,最低种植成本为100(元/100kg) …13分.
点评:本题考查了二次函数模型的应用,考查利用二次函数的图象与性质求函数的最值问题,确定函数模型是关键.

练习册系列答案
相关题目
(
)
,53,(
)-2的大小关系是( )
| 1 |
| 5 |
| 2 |
| 5 |
| 1 |
| 3 |
A、(
| ||||||
B、(
| ||||||
C、(
| ||||||
D、(
|
设M=
,N=
,P=
,Q
,则M与N、P与Q的大小关系为( )
| 102012+1 |
| 102013+1 |
| 102013+1 |
| 102014+1 |
| 102012+9 |
| 102013+100 |
| 102013+9 |
| 102014+100 |
| A、M>N,P<Q |
| B、M>N,P<Q |
| C、M>N,P<Q |
| D、M>N,P<Q |
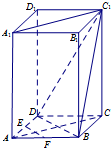 在长方体ABCD-A1B1C1D1中,底面ABCD为正方形,E,F分别为棱AD、,AB的中点.
在长方体ABCD-A1B1C1D1中,底面ABCD为正方形,E,F分别为棱AD、,AB的中点.