题目内容
若不等式x2-kx+k＞0对任意的x∈R恒成立，则实数k的取值范围是 ．
考点：二次函数的性质,函数恒成立问题
专题：函数的性质及应用
分析：不等式x2-kx+k＞0恒成立，则函数y=x2-kx+k的图象都在x轴的上方，得到判别式小于0．
解答：
解：因为不等式x2-kx+k＞0恒成立，则函数y=x2-kx+k的图象都在x轴的上方，
所以判别式△=k2-4k＜0，解得0＜k＜4；
故答案为：（0，4）
所以判别式△=k2-4k＜0，解得0＜k＜4；
故答案为：（0，4）
点评：本题考查了一元二次不等式恒成立问题求参数范围；关键是与二次函数结合，得到判别式与0的不等式．
练习册系列答案
鸿图图书寒假作业假期作业吉林大学出版社系列答案
相关题目
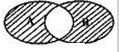如图所示的韦恩图中，A，B是非空集合，定义集合A*B为阴影部分表示的集合，若x，y∈R，A={x|y=设全集为R，集合A={x|
≥0}，B={x|-2≤x＜0}，则（∁RA）∩B等于（ ）
| x-1 |
| x+1 |
| A、（-1，0） |
| B、[-1，0） |
| C、[-2，-1] |
| D、[-2，-1） |
如图，设椭圆C：