题目内容
若点O是线段BC外一点,点P是平面上任意一点,且
=λ
+μ
(λ,μ∈R),则下列说法正确的有
①若λ+μ=1且λ>0,则点P在线段BC的延长线上;
②若λ+μ=1且λ<0,则点P在线段BC的延长线上;
③若λ+μ>1,则点P在△OBC外;
④若λ+μ<1,则点P在△OBC内.
| OP |
| OB |
| OC |
①若λ+μ=1且λ>0,则点P在线段BC的延长线上;
②若λ+μ=1且λ<0,则点P在线段BC的延长线上;
③若λ+μ>1,则点P在△OBC外;
④若λ+μ<1,则点P在△OBC内.
考点:平面向量的基本定理及其意义
专题:平面向量及应用
分析:根据向量的减法运算,向量数乘的几何意义,向量加法的平行四边形法则,以及相反向量的概念即可判断出每一项的正误.
解答:
解:因为
=λ
+μ
(λ,μ∈R)
①若λ+μ=1且λ>0,
=λ
+(1-λ)
=
+λ(
-
)故
-
=λ(
-
)即
=λ
又λ>0则点P在线段BC或其反向延长线上,错误;
②若λ+μ=1且λ<0,同上可得
=λ
而λ<0则点P在线段BC的延长线上,正确;
③若λ+μ>1,
=λ
+(1-λ)
+(λ+μ-1)
,同上可得
=λ
+(λ+μ-1)
,当λ+μ>1时,λ+μ-1>0根据向量加法的平行四边形法则可以看出则点P在△OBC外,正确;
④若λ+μ<1,不防令λ=0,μ=-1则
=-
,很显然此时点P在线段CO的延长线上,不在△OBC内,错误.
所以说法正确的有:②③.
故答案为:②③.
| OP |
| OB |
| OC |
①若λ+μ=1且λ>0,
| OP |
| OB |
| OC |
| OC |
| OB |
| OC |
| OP |
| OC |
| OB |
| OC |
| CP |
| CB |
②若λ+μ=1且λ<0,同上可得
| CP |
| CB |
③若λ+μ>1,
| OP |
| OB |
| OC |
| OC |
| CP |
| CB |
| OC |
④若λ+μ<1,不防令λ=0,μ=-1则
| OP |
| OC |
所以说法正确的有:②③.
故答案为:②③.
点评:考查向量的减法运算,向量数乘的几何意义,向量加法的平行四边形法则,以及相反向量的概念.

练习册系列答案
 轻松暑假总复习系列答案
轻松暑假总复习系列答案
相关题目
已知双曲线方程为x2-
=1,过P(1,2)的直线L与双曲线只有一个公共点,则L的条数共有( )
| y2 |
| 4 |
| A、4条 | B、3条 | C、2条 | D、1条 |
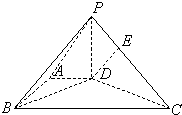 如图,在底面为直角梯形的四棱锥P-ABCD中,AD∥BC,PD⊥平面ABCD,AD=1,AB=
如图,在底面为直角梯形的四棱锥P-ABCD中,AD∥BC,PD⊥平面ABCD,AD=1,AB=| 3 |
(1)求证:BD⊥PC;
(2)设点E在棱PC上,
| FE |
| FC |
一个几何体的三视图如图所示,则它的体积为( )


A、
| ||
B、
| ||
| C、20 | ||
| D、40 |
已知研究x与y之间关系的一组数据如表所示,则y对x的回归直线方程
=bx+a必过点( )
 |
| y |
| x | 0 | 1 | 2 | 3 |
| y | 1 | 3 | 5 | 7 |
| A、(2,2) | ||
B、(
| ||
| C、(1,2) | ||
D、(
|