题目内容
19.已知sinα=-$\frac{4}{5}$且$\frac{π}{2}$<α<$\frac{3π}{2}$.(1)求cosα的值;
(2)求$\frac{sin(\frac{π}{2}-α)cos(-α-π)tan(π-α)}{sin(-π+α)cos(\frac{π}{2}+α)}$的值.
分析 (1)利用同角三角函数的基本关系式求解即可.
(2)利用诱导公式化简表达式然后求解函数值即可.
解答 解:(1)sinα=-$\frac{4}{5}$且$\frac{π}{2}$<α<$\frac{3π}{2}$.
cosα=-$\sqrt{1-{sin}^{2}α}$=-$\frac{3}{5}$;
(2)$\frac{sin(\frac{π}{2}-α)cos(-α-π)tan(π-α)}{sin(-π+α)cos(\frac{π}{2}+α)}$
=$\frac{cosαcosαtanα}{sinαsinα}$
=$\frac{cosα}{sinα}$
=$\frac{-\frac{3}{5}}{-\frac{4}{5}}$
=$\frac{3}{4}$.
点评 本题考查三角函数的化简求值,诱导公式的应用,考查计算能力.

练习册系列答案
 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案
相关题目
7.已知直线l:kx-y+1-k=0与圆O:x2+y2=8交于P,Q两点,若圆O上有一个点E,使得OPEQ是平行四边形,则弦PQ的长为( )
| A. | 2$\sqrt{2}$ | B. | 2$\sqrt{3}$ | C. | 2$\sqrt{6}$ | D. | 2$\sqrt{10}$ |
5.公比为2的等比数列{an} 的各项都是正数,且a3a11=16,则a5=( )
| A. | 4 | B. | 2 | C. | 1 | D. | 8 |
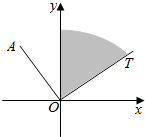 如图所示,在直角坐标系内,射线OT落在30°角的终边上,任作一条射线OA,则射线OA落在∠yOT内的概率为$\frac{1}{6}$.
如图所示,在直角坐标系内,射线OT落在30°角的终边上,任作一条射线OA,则射线OA落在∠yOT内的概率为$\frac{1}{6}$. 在某高校自主招生考试中,所有选报II类志向的考生全部参加了“数学与逻辑”和“阅读与表达”两个科目的考试,成绩分为A,B,C,D,E五个等级.某考场考生的两科考试成绩数据统计如下图所示,其中“数学与逻辑”科目的成绩为B的考生有10人.
在某高校自主招生考试中,所有选报II类志向的考生全部参加了“数学与逻辑”和“阅读与表达”两个科目的考试,成绩分为A,B,C,D,E五个等级.某考场考生的两科考试成绩数据统计如下图所示,其中“数学与逻辑”科目的成绩为B的考生有10人.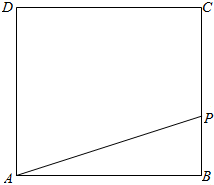 分别根据下列两个实际背景
分别根据下列两个实际背景