题目内容
10.已知y=x2+2ax+1(1)若当x∈[-1,2]时,y的最大值为4,求a.
(2)若当a∈[-1,2]时,y的最大值为4,求x.
分析 (1)根据一元二次函数的性质结合函数的最值性进行求解.
(2)利用参数转化法构造函数g(a),利用一次函数的性质进行求解即可.
解答 解:(1)设y=f(x),则f(x)=(x+a)2+1-a2
当|-a-(-1)|≥|-a-2|即$a≤-\frac{1}{2}$时,f(x)max=f(-1)=2-2a=4,
解得:a=-1
当|-a-(-1)|<|-a-2|即$a>-\frac{1}{2}$时,f(x)max=f(2)=5+4a=4,
解得:$a=-\frac{1}{4}$∴$a=-1或a=-\frac{1}{4}$…6
(2)设y=g(a),则g(a)=2xa+(x2+1)
当2x=0即x=0时,g(a)=1不符合题设,舍去
当2x>0即x>0时,$g{(a)_{max}}=g(2)={x^2}+4x+1=4$
解得:$x=-2+\sqrt{7}$或$x=-2-\sqrt{7}$(舍)
当2x<0即x<0时,$g{(a)_{max}}=g(-1)={x^2}-2x+1=4$
解得:x=3(舍)或x=-1,
∴$x=-2+\sqrt{7}或x=-1$…12
点评 本题主要考查一元二次函数的性质,对于含有参数的数学问题,一般使用参数转化法进行求解.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
15.要得到函数y=-cos2x的图象,只需将函数y=sin(2x-$\frac{π}{4}$)的图象( )
| A. | 向右平移$\frac{π}{8}$个单位 | B. | 向左平移$\frac{π}{8}$个单位 | ||
| C. | 向左平移$\frac{π}{4}$个单位 | D. | 向右平移$\frac{π}{4}$个单位 |
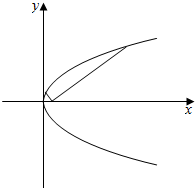 已知顶点在原点,焦点F在x轴上的抛物线过点A(9,6).
已知顶点在原点,焦点F在x轴上的抛物线过点A(9,6).