Question

9．分别根据下列两个实际背景
（1）求函数f（x）的解析式；
（2）画出函数f（x） 的图象；
（3）求函数f（x）的值域．
背景1：在国内投递外埠平信，每封信不超过20g付邮资80分，超过20g不超过40g付邮资160分，超过40g不超过60g付邮资240，依此类推，每xg（0＜x≤100）的信应付邮资f（x）（单位：分）．
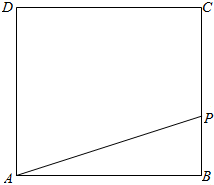
背景2：如图所示，在边长为2的正方形ABCD的边上有一个动点P，从点A出发沿折线．ABCD移动一周后，回到A点．设点A移动的路程为x，△PAC的面积为f（x）．

Answer 1

分析 （1）由题意利用分段函数的知识，分类讨论求得函数f（x）的解析式．
（2）由题意结合函数的解析式作出函数的图象．
（3）结合函数的图象，求出函数的值域．

解答 解：（1）背景1：函数f（x）=$\left\{\begin{array}{l}{80，0＜x≤20}\\{160，20＜x≤40}\\{240，40＜x≤60}\\{320，60＜x≤80}\\{400，80＜x≤100}\end{array}\right.$，
背景2：当点P在线段AB上时，x∈[0，2），△PAC的面积为f（x）=$\frac{1}{2}•x•2$=x；
当点P在线段BC上时，x∈[2，4），△PAC的面积为f（x）=$\frac{1}{2}$•（x-2）•2=x-2；
当点P在线段CD上时，x∈[4，6），△PAC的面积为f（x）=$\frac{1}{2}$•（x-4）•2=x-4；
当点P在线段DA上时，x∈[6，8），△PAC的面积为f（x）=$\frac{1}{2}$•（8-x）•2=8-x，
综合可得，f（x）=$\left\{\begin{array}{l}{x，x∈[0，2]}\\{x-2，x∈（2，4]}\\{x-4，x∈（4，6]}\\{8-x，x∈（6，8]}\end{array}\right.$．
（2）背景1与背景2中，函数f（x）的图象如图所示：

（3）结合背景1中函数f（x）的图象，可得函数的值域为{80，160，240，320，400}．
结合背景2中函数f（x）的图象，可得函数的值域为[0，2]．

点评 本题主要考查分段函数的应用，函数的图象特征，体现了分类讨论、转化的数学思想，属于中档题．