题目内容
在极坐标系中,曲线C:ρ=2cosθ.以极点为原点,极轴为x轴的正半轴建立平面直角坐标系,直线l的参数方程为
(t为参数),直线l与曲线C分别交于点M,N.写出曲线C的直角坐标方程并求出线段MN的长度.
|
考点:简单曲线的极坐标方程
专题:坐标系和参数方程
分析:把极坐标方程化为直角坐标方程,再把参数方程代入,求得t的值,根据参数的几何意义求得线段MN的长度.
解答:
解:曲线C:ρ=2cosθ可化为ρ2=2ρcosθ,可得曲线C的直角坐标方程为x2+y2=2x.
把直线l的参数方程为
代入x2+y2=2x 可得
+
=
t,求得t=0,或 t=
.
由t的几何意义可得线段MN的长度为
.
把直线l的参数方程为
|
| t2 |
| 2 |
| t2 |
| 2 |
| 2 |
| 2 |
由t的几何意义可得线段MN的长度为
| 2 |
点评:本题主要考查把参数方程、极坐标方程化为直角坐标方程的方法,参数的几何意义,属于基础题.

练习册系列答案
 培优三好生系列答案
培优三好生系列答案 优化作业上海科技文献出版社系列答案
优化作业上海科技文献出版社系列答案
相关题目
设i是虚数单位,复数z满足
=
,则复数z的共轭复数为( )
| z |
| i |
| 5 |
| i-2 |
| A、-1-2i | B、-1+2i |
| C、1+2i | D、1-2i |
设f(x)是定义在R上的奇函数,当x≤0时,f(x)=2x-b(为常数),则f(1)=( )
| A、-1 | ||
B、-
| ||
C、
| ||
| D、1 |
为得到函数y=cosx的图象,只需将函数y=sinx的图象按照向量
平移,则
可以为( )
| a |
| a |
A、(
| ||
B、(-
| ||
C、(0,-
| ||
D、(0,
|
 如图,某工厂生产的一种无盖冰淇淋纸筒为圆锥形,现一客户订制该圆锥纸筒,并要求该圆锥纸筒的容积为π.设圆锥纸筒底面半径为r,高为h.
如图,某工厂生产的一种无盖冰淇淋纸筒为圆锥形,现一客户订制该圆锥纸筒,并要求该圆锥纸筒的容积为π.设圆锥纸筒底面半径为r,高为h. 甲、乙两名运动员为了争取得到2016年巴西奥运会的最后一个参赛名额,共进行了7轮比赛,得分情况如茎叶图所示.
甲、乙两名运动员为了争取得到2016年巴西奥运会的最后一个参赛名额,共进行了7轮比赛,得分情况如茎叶图所示.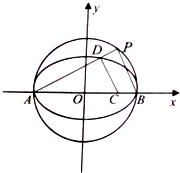 已知椭圆E:
已知椭圆E: