题目内容
已知P(x,y)为函数y=1+lnx图象上一点,O为坐标原点,记直线OP的斜率k=f(x).
(Ⅰ)求函数f(x)的单调区间;
(Ⅱ)设F(x)=x+
-f(x),求函数F(x)的最小值.
(Ⅰ)求函数f(x)的单调区间;
(Ⅱ)设F(x)=x+
| 1 |
| x |
考点:利用导数求闭区间上函数的最值,利用导数研究函数的单调性
专题:导数的综合应用
分析:(Ⅰ)利用导数法即可求得函数的单调区间;
(Ⅱ)由题意得F(x)=x-
,利用导数判断函数的单调性,即可求得函数的最小值.
(Ⅱ)由题意得F(x)=x-
| lnx |
| x |
解答:
解:(Ⅰ)由题意得f(x)=
,x>0,
∴f′(x)=(
)′=-
,
当lnx>0即x>1时,f′(x)<0;当0<x<1时,f′(x)>0,
∴f(x)在(0,1)上单调递增,在(1,+∞)上单调递减.
(Ⅱ)F(x)=x+
-f(x)=x+
-
=x-
,
∴F′(x)=
,
设h(x)=x2-1+lnx,则h′(x)=2x+
>0(x>0),
∴h(x)在(0,+∞)上是增函数,
又h(1)=0,∴F′(1)=0且F′(x)有唯一的零点1,
∴F(x)在(0,1)上是单调减函数,在[1,+∞)为增函数,
∴函数F(x)的最小值为F(1)=1.
| 1+lnx |
| x |
∴f′(x)=(
| 1+lnx |
| x |
| lnx |
| x2 |
当lnx>0即x>1时,f′(x)<0;当0<x<1时,f′(x)>0,
∴f(x)在(0,1)上单调递增,在(1,+∞)上单调递减.
(Ⅱ)F(x)=x+
| 1 |
| x |
| 1 |
| x |
| 1+lnx |
| x |
| lnx |
| x |
∴F′(x)=
| x2-1+lnx |
| x2 |
设h(x)=x2-1+lnx,则h′(x)=2x+
| 1 |
| x |
∴h(x)在(0,+∞)上是增函数,
又h(1)=0,∴F′(1)=0且F′(x)有唯一的零点1,
∴F(x)在(0,1)上是单调减函数,在[1,+∞)为增函数,
∴函数F(x)的最小值为F(1)=1.
点评:本题主要考查利用导数研究函数的单调性、求单调区间及最值问题,考查学生的运算能力,属中档题.

练习册系列答案
相关题目
已知i是虚数单位,复数z=-i,则
的虚部为( )
| 1 |
| 1-z |
A、
| ||
B、
| ||
C、-
| ||
D、-
|
若向量
=(4,y)(y∈R),则“y=3”是“|
|=5”的( )
| a |
| a |
| A、充分而不必要条件 |
| B、必要而不充分条件 |
| C、充要条件 |
| D、既不充分又不必要条件 |
将函数f(x)=x3+3x2+3x的图象按向量
平移后得到函数g(x)的图象,若函数g(x)满足g(1-x)+g(1+x)=1,则向量
的坐标是( )
| a |
| a |
| A、(-1,-1) | ||
B、(2,
| ||
| C、(2,2) | ||
D、(-2,-
|
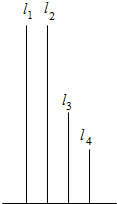
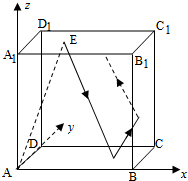 如图,在长方体ABCD-A1B1C1D1中,AB=11,AD=7,AA1=12.一质点从顶点A射向点E(4,3,12),遇长方体的面反射(反射服从光的反射原理),将第i-1次到第i次反射点之间的线段记为li(i=2,3,4),l1=AE,将线段l1,l2,l3,l4竖直放置在同一水平线上,则大致的图形是( )
如图,在长方体ABCD-A1B1C1D1中,AB=11,AD=7,AA1=12.一质点从顶点A射向点E(4,3,12),遇长方体的面反射(反射服从光的反射原理),将第i-1次到第i次反射点之间的线段记为li(i=2,3,4),l1=AE,将线段l1,l2,l3,l4竖直放置在同一水平线上,则大致的图形是( )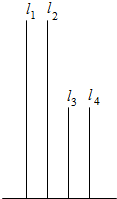


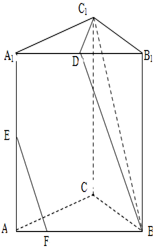 在正三棱柱ABC-A1B1C1中,AB=AA1,D、E分别是棱A1B1、AA1的中点,点F在棱AB上,且AB=4AF.
在正三棱柱ABC-A1B1C1中,AB=AA1,D、E分别是棱A1B1、AA1的中点,点F在棱AB上,且AB=4AF. 如图,已知椭圆E:
如图,已知椭圆E: