题目内容
甲、乙两名运动员为了争取得到2016年巴西奥运会的最后一个参赛名额，共进行了7轮比赛，得分情况如茎叶图所示．（Ⅰ）根据茎叶图分别甲、乙两名运动员中哪位的比赛成绩更为稳定？
（Ⅱ）若分别从甲、乙两名运动员的7轮比赛不低于80且不高于90的得分中任选1个，求甲、乙两名运动员得分之差的绝对值ξ的分布列及数学期望．
考点：离散型随机变量的期望与方差,茎叶图
专题：概率与统计
分析：（Ⅰ）用公式计算甲、乙运动员的平均分与方差，比较后可得结论；
（II）确定ξ的可能取值，计算相应的概率，从而可得ξ的分布列与期望．
（II）确定ξ的可能取值，计算相应的概率，从而可得ξ的分布列与期望．
解答：
解：（Ⅰ）甲运动员的平均分
=
=84，
方差s甲2=
=
；
乙运动员的平均分
=
=85，
方差s乙2=
=
；
∵
＜
，
∴乙运动员的比赛成绩更为稳定．
（2）设甲、乙两名运动员的得分分别为x，y，则得分之差的绝对值为ξ=|x-y|．
显然，由茎叶图可知，ξ的可能取值为0，1，2，3，5，6．
当ξ=0时，x=y=84，故P（ξ=0）=
=
；
当ξ=1时，x=85，y=84或y=86，故P（ξ=1）=
=
；
当ξ=2时，x=84，y=86或x-85，y=87，故P（ξ=2）=
+
=
；
当ξ=3时，x=81，y=84或x=84，y=87，故P（ξ=3）=
+
=
=
；
当ξ=5时，x=81，y=86，故P（ξ=5）=
=
；
当ξ=6时，x=81，y=87，故P（ξ=6）=
=
；
所以ξ的分布列为：
Eξ=0×
+1×
+2×
+3×
+5×
+6×
=
. |
| x甲 |
| 78+81+84+85+84+85+91 |
| 7 |
方差s甲2=
| (78-84)2+(81-84)2+(84-84)2+(85-84)2+(84-84)2+(85-84)2+(91-84)2 |
| 7 |
| 96 |
| 7 |
乙运动员的平均分
. |
| x乙 |
| 79+84+84+86+87+84+91 |
| 7 |
方差s乙2=
| (79-84)2+(84-84)2+(84-84)2+(86-84)2+(87-84)2+(84-84)2+(91-84)2 |
| 7 |
| 87 |
| 7 |
∵
| 87 |
| 7 |
| 96 |
| 7 |
∴乙运动员的比赛成绩更为稳定．
（2）设甲、乙两名运动员的得分分别为x，y，则得分之差的绝对值为ξ=|x-y|．
显然，由茎叶图可知，ξ的可能取值为0，1，2，3，5，6．
当ξ=0时，x=y=84，故P（ξ=0）=
| ||||
|
| 6 |
| 25 |
当ξ=1时，x=85，y=84或y=86，故P（ξ=1）=
| ||||
|
| 8 |
| 25 |
当ξ=2时，x=84，y=86或x-85，y=87，故P（ξ=2）=
| ||||
|
| ||||
|
| 4 |
| 25 |
当ξ=3时，x=81，y=84或x=84，y=87，故P（ξ=3）=
| ||||
|
| ||||
|
| 5 |
| 25 |
| 1 |
| 5 |
当ξ=5时，x=81，y=86，故P（ξ=5）=
| ||||
|
| 1 |
| 25 |
当ξ=6时，x=81，y=87，故P（ξ=6）=
| ||||
|
| 1 |
| 25 |
所以ξ的分布列为：
| ξ | 0 | 1 | 2 | 3 | 5 | 6 | ||||||||||||
| P |
|
|
|
|
|
|
| 6 |
| 25 |
| 8 |
| 25 |
| 4 |
| 25 |
| 1 |
| 5 |
| 1 |
| 25 |
| 1 |
| 25 |
| 42 |
| 25 |
点评：本题考查平均数与方差的计算，茎叶图，考查离散型随机变量的分布列与数学期望，确定的取值，计算概率是关键．
练习册系列答案
相关题目
已知x、y满足
，则z=
的取值范围为（ ）
|
| y-1 |
| x+2 |
A、[0，
| ||
| B、[0，1] | ||
C、（-∞，
| ||
D、[
|
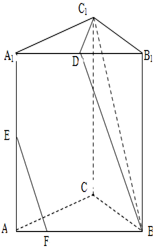在正三棱柱ABC-A1B1C1中，AB=AA1，D、E分别是棱A1B1、AA1的中点，点F在棱AB上，且AB=4AF．