题目内容
 如图,某工厂生产的一种无盖冰淇淋纸筒为圆锥形,现一客户订制该圆锥纸筒,并要求该圆锥纸筒的容积为π.设圆锥纸筒底面半径为r,高为h.
如图,某工厂生产的一种无盖冰淇淋纸筒为圆锥形,现一客户订制该圆锥纸筒,并要求该圆锥纸筒的容积为π.设圆锥纸筒底面半径为r,高为h.(1)求出r与h满足的关系式;
(2)工厂要求制作该纸筒的材料最省,求最省时
| h |
| r |
考点:旋转体(圆柱、圆锥、圆台)
专题:导数的综合应用,空间位置关系与距离
分析:(1)设圆锥纸筒的容积为V,则V=
πr2h,进而由圆锥纸筒的容积为π,得到r与h满足的关系式;
(2)工厂要求制作该纸筒的材料最省,即所用材料的面积最小,即要该圆锥的侧面积最小,求出圆锥侧面积的表达式,利用导数法,求出h=
时S最小,进而得到答案.
| 1 |
| 3 |
(2)工厂要求制作该纸筒的材料最省,即所用材料的面积最小,即要该圆锥的侧面积最小,求出圆锥侧面积的表达式,利用导数法,求出h=
| 3 | 6 |
解答:
解:(1)设圆锥纸筒的容积为V,则V=
πr2h,
由该圆锥纸筒的容积为π,则
πr2h=π,即r2h=3,
故r与h满足的关系式为r2h=3; …(4分)
(2)工厂要求制作该纸筒的材料最省,即所用材料的面积最小,即要该圆锥的侧面积最小,
设该纸筒的侧面积为S,则S=πrl,其中l为圆锥的母线长,且l=
,
所以S=πr
=π
=π
=π
,(h>0 ),…(8分)
设f(h)=
+3h (h>0 ),
由f′(h)=-
+3=0,解得h=
,
当0<h<
时,f′(h)<0;当h>
时,f′(h)>0;
因此,h=
时f(h)取得极小值,且是最小值,此时S亦最小;…(12分)
由r2h=3得
=
=
=
=
,
所以最省时
的值为
. …(14分)
| 1 |
| 3 |
由该圆锥纸筒的容积为π,则
| 1 |
| 3 |
故r与h满足的关系式为r2h=3; …(4分)
(2)工厂要求制作该纸筒的材料最省,即所用材料的面积最小,即要该圆锥的侧面积最小,
设该纸筒的侧面积为S,则S=πrl,其中l为圆锥的母线长,且l=
| r2+h2 |
所以S=πr
| r2+h2 |
| (r2+h2)r2 |
(
|
|
设f(h)=
| 9 |
| h2 |
由f′(h)=-
| 18 |
| h3 |
| 3 | 6 |
当0<h<
| 3 | 6 |
| 3 | 6 |
因此,h=
| 3 | 6 |
由r2h=3得
| h |
| r |
|
|
|
| 2 |
所以最省时
| h |
| r |
| 2 |
点评:本题考查的知识点是旋转体,导数法求函数的最值,是立体几何与导数的综合应用,难度中档.

练习册系列答案
相关题目
若x,y满足约束条件
,则2x-y的最小值为( )
|
| A、-6 | B、-4 | C、-3 | D、-1 |
将函数f(x)=x3+3x2+3x的图象按向量
平移后得到函数g(x)的图象,若函数g(x)满足g(1-x)+g(1+x)=1,则向量
的坐标是( )
| a |
| a |
| A、(-1,-1) | ||
B、(2,
| ||
| C、(2,2) | ||
D、(-2,-
|
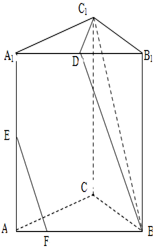 在正三棱柱ABC-A1B1C1中,AB=AA1,D、E分别是棱A1B1、AA1的中点,点F在棱AB上,且AB=4AF.
在正三棱柱ABC-A1B1C1中,AB=AA1,D、E分别是棱A1B1、AA1的中点,点F在棱AB上,且AB=4AF.