题目内容
 已知椭圆E:
已知椭圆E:| x2 |
| a2 |
| y2 |
| b2 |
| ||
| 2 |
(Ⅰ)求椭圆E的方程;
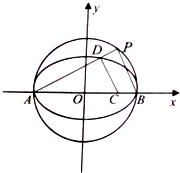
(Ⅱ)若点P是圆x2+y2=4上一动点,且在x轴上方,连接PA交椭圆E于点D,已知点C(1,0),设直线PB,DC的斜率分别为k1,k2,且k1=λk2,求λ的取值范围.
考点:直线与圆锥曲线的综合问题
专题:圆锥曲线中的最值与范围问题
分析:(1)由题意可得
,解出a,b,c即可.
(2)利用斜率计算公式、相互垂直的直线斜率之间的关系、点与椭圆的关系即可得出.
|
(2)利用斜率计算公式、相互垂直的直线斜率之间的关系、点与椭圆的关系即可得出.
解答:
解:(1)由题意可得
,解得a=2,b=1,c=
.
故椭圆E的方程为
+y2=1.
(2)设D(x1,y1),则k2=
,kPA=kDA=
,
又PA⊥PB,∴k1=-
.
又
=1-
,
∴λ=
=-
×
=-
=
=4(1+
),
由x1∈(-2,2)得λ<3且λ≠0,
故λ的取值范围是(-∞,0)∪(0,3).
|
| 3 |
故椭圆E的方程为
| x2 |
| 4 |
(2)设D(x1,y1),则k2=
| y1 |
| x1-1 |
| y1 |
| x1+2 |
又PA⊥PB,∴k1=-
| x1+2 |
| y1 |
又
| y | 2 1 |
| ||
| 4 |
∴λ=
| k1 |
| k2 |
| x1+2 |
| y1 |
| x1-1 |
| y1 |
| (x1+2)(x1-1) | ||||
1-
|
| 4(x1-1) |
| x1-2 |
| 1 |
| x1-2 |
由x1∈(-2,2)得λ<3且λ≠0,
故λ的取值范围是(-∞,0)∪(0,3).
点评:本题考查了椭圆与的标准方程及其性质、斜率计算公式、相互垂直的直线斜率之间的关系等基础知识与基本技能方法,考查了推理能力和计算能力,属于难题.

练习册系列答案
 状元坊全程突破导练测系列答案
状元坊全程突破导练测系列答案
相关题目
 如图,已知椭圆E:
如图,已知椭圆E: