题目内容
已知函数f(x)=ax-2,g(x)=loga|x|(其中a>0且a≠1),若f(4)•g(-4)<0,则f(x),g(x)在同一坐标系内的大致图象是( )
A、 |
B、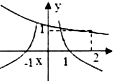 |
C、 |
D、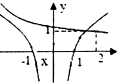 |
考点:函数的图象
专题:函数的性质及应用
分析:利用条件f(4)g(-4)<0,确定a的大小,从而确定函数的单调性.
解答:
解:由题意f(x)=ax-2是指数型的,g(x)=loga|x|是对数型的且是一个偶函数,
由f(4)•g(-4)<0,可得出g(-4)<0,由此特征可以确定C、D两选项不正确,
由g(-4)<0得loga4<0,∴0<a<1,故其底数a∈(0,1),由此知f(x)=ax-2,是一个减函数,由此知A不对,B选项是正确答案
故选:B.
由f(4)•g(-4)<0,可得出g(-4)<0,由此特征可以确定C、D两选项不正确,
由g(-4)<0得loga4<0,∴0<a<1,故其底数a∈(0,1),由此知f(x)=ax-2,是一个减函数,由此知A不对,B选项是正确答案
故选:B.
点评:本题主要考查了函数图象的识别和应用.判断函数图象要充分利用函数本身的性质,由f(4)•g(-4)<0,利用指数函数和对数函数的性质是解决本题的关键.

练习册系列答案
相关题目
复数
等于( )
| 3+i |
| 1+i |
| A、1+2i | B、1-2i |
| C、2-i | D、2+i |
已知等差数列{an},a6=2,则此数列的前11项的和S11=( )
| A、44 | B、33 | C、22 | D、11 |
某校高三年级学生会主席团有共有5名同学组成,其中有3名同学来自同一班级,另外两名同学来自另两个不同班级.现从中随机选出两名同学参加会议,则两名选出的同学来自不同班级的概率为( )
| A、0.35 | B、0.4 |
| C、0.6 | D、0.7 |
函数y=ax-b(a>0且a≠1)的图象不经过第一象限,则( )
| A、a>1且b<-1 |
| B、a<1且b<-1 |
| C、a<1且b≥1 |
| D、a<1且b≤1 |
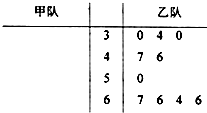 甲、乙两个竞赛队都参加了10场比赛,比赛得分情况记录如下(单位:分):
甲、乙两个竞赛队都参加了10场比赛,比赛得分情况记录如下(单位:分):