题目内容
已知等差数列{an},a6=2,则此数列的前11项的和S11=( )
| A、44 | B、33 | C、22 | D、11 |
考点:等差数列的通项公式
专题:等差数列与等比数列
分析:由等差数列的通项公式和性质可得S11=11a6,代值计算可得.
解答:
解:∵等差数列{an},a6=2,
∴数列的前11项的和S11=
=
=11a6=22
故选:C
∴数列的前11项的和S11=
| 11(a1+a11) |
| 2 |
=
| 11×2a6 |
| 2 |
故选:C
点评:本题考查等差数列的通项公式和性质,属基础题.

练习册系列答案
 口算题天天练系列答案
口算题天天练系列答案
相关题目
 已知三棱锥S-ABC的所有顶点都在球O的球面上,SA⊥平面ABC,AB⊥BC且AB=BC=1,SA=
已知三棱锥S-ABC的所有顶点都在球O的球面上,SA⊥平面ABC,AB⊥BC且AB=BC=1,SA=| 2 |
| A、4π | ||
B、
| ||
| C、3π | ||
D、
|
函数f(x)的零点与g(x)=4x+2x-2的零点之差的绝对值不超过0.25,则f(x)可能是( )
| A、f(x)=(x-1)2 | ||
| B、f(x)=4x-1 | ||
C、f(x)=ln(x-
| ||
| D、f(x)=ex-1 |
公比为
的等比数列{an}的各项都是正数,且a4a6=16,则a7=( )
| 1 |
| 2 |
A、
| ||
| B、1 | ||
| C、2 | ||
| D、4 |
已知两个单位向量
,
的夹角为45°,且满足
⊥(λ
-
),则实数λ的值为( )
| e1 |
| e2 |
| e1 |
| e2 |
| e1 |
| A、1 | ||||
B、
| ||||
C、
| ||||
| D、2 |
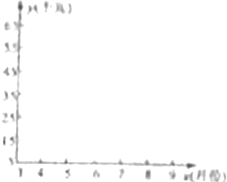 某公司生产部门调研发现,该公司第二、三季度的用电量与月份线性相关,数据统计如表:
某公司生产部门调研发现,该公司第二、三季度的用电量与月份线性相关,数据统计如表:


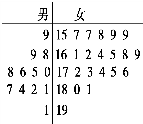 某学校举行元旦晚会,组委会招募了12名男志愿者和18名女志愿者,将这30名志愿者的身高编成如图所示的茎叶图(单位:cm)身高175cm以上(包括175cm)定义为“高个子”,身高在175cm以下(不包括175cm)定义为“非高个子”.
某学校举行元旦晚会,组委会招募了12名男志愿者和18名女志愿者,将这30名志愿者的身高编成如图所示的茎叶图(单位:cm)身高175cm以上(包括175cm)定义为“高个子”,身高在175cm以下(不包括175cm)定义为“非高个子”.