题目内容
某校高三年级学生会主席团有共有5名同学组成，其中有3名同学来自同一班级，另外两名同学来自另两个不同班级．现从中随机选出两名同学参加会议，则两名选出的同学来自不同班级的概率为（ ）
| A、0.35 | B、0.4 |
| C、0.6 | D、0.7 |
考点：古典概型及其概率计算公式,互斥事件的概率加法公式,相互独立事件的概率乘法公式
专题：概率与统计
分析：分别计算出从5名学生中选出2名学生进入学生会的基本事件总数和满足这两名选出的同学来自不同班级的基本事件个数，代入古典概型概率计算公式，可得答案
解答：
解：来自同一班级的3名同学，用1，2，3表示，来自另两个不同班级2名同学用，A，B表示，
从中随机选出两名同学参加会议，共有12，13，1A，1B，23，2A，2B，3A，3B，AB共10种，
这两名选出的同学来自不同班级，共有1A，1B，23，2A，2B，3A，3B共7种，
故这两名选出的同学来自不同班级概率P=
=0.7
故选：D．
从中随机选出两名同学参加会议，共有12，13，1A，1B，23，2A，2B，3A，3B，AB共10种，
这两名选出的同学来自不同班级，共有1A，1B，23，2A，2B，3A，3B共7种，
故这两名选出的同学来自不同班级概率P=
| 7 |
| 10 |
故选：D．
点评：本题考查的知识点是古典概型概率计算公式，其中熟练掌握利用古典概型概率计算公式求概率的步骤，是解答的关键．
练习册系列答案
相关题目
函数f（x）的零点与g（x）=4x+2x-2的零点之差的绝对值不超过0.25，则f（x）可能是（ ）
| A、f（x）=（x-1）2 | ||
| B、f（x）=4x-1 | ||
C、f（x）=ln（x-
| ||
| D、f（x）=ex-1 |
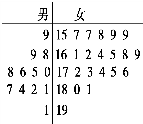某学校举行元旦晚会，组委会招募了12名男志愿者和18名女志愿者，将这30名志愿者的身高编成如图所示的茎叶图（单位：cm）身高175cm以上（包括175cm）定义为“高个子”，身高在175cm以下（不包括175cm）定义为“非高个子”．