题目内容
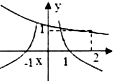
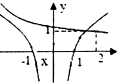
函数y=ax-b（a＞0且a≠1）的图象不经过第一象限，则（ ）
| A、a＞1且b＜-1 |
| B、a＜1且b＜-1 |
| C、a＜1且b≥1 |
| D、a＜1且b≤1 |
考点：指数函数的图像变换
专题：函数的性质及应用
分析：根据指数函数的图象和性质进行判断．
解答：
解：若函数y=ax-b（a＞0且a≠1）的图象不经过第一象限，
则函数为减函数，则0＜a＜1，且y=f（0）≤0，
即a0-b≤0，
即b≥1，
综上a＜1且b≥1，
故选：C
则函数为减函数，则0＜a＜1，且y=f（0）≤0，
即a0-b≤0，
即b≥1，
综上a＜1且b≥1，
故选：C
点评：本题主要考查指数函数的图象和性质，利用数形结合是解决本题的关键．
练习册系列答案
灵星计算小达人系列答案
孟建平错题本系列答案
相关题目
已知a，b∈R，则“a＞b＞1”是“logab＜1”的（ ）
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充要条件 |
| D、既不充分也不必要条件 |