题目内容
写出由方程ax2-（a+1）x+a=0的解组成的集合中的元素．
考点：集合的表示法,元素与集合关系的判断
专题：集合
分析：对a分类讨论：当a=0时，当a≠0时，△=（a+1）2-4a2=-（3a+1）（a-1）．再分当△＞0时，当△=0时，当△＜0时，三种情况讨论即可得出．
解答：
解：当a=0时，方程ax2-（a+1）x+a=0化为-x=0，解得x=0，此时方程的解组成的集合为{0}；
当a≠0时，△=（a+1）2-4a2=-（3a+1）（a-1）．
当△＞0时，解得-
＜a＜1，且a≠0，由方程ax2-（a+1）x+a=0解得x=
，
此时方程的解组成的集合为{
，
}；
当△=0时，解得a=-
或1，当a=1时，此时方程的解组成的集合为{1}；当a=-
时，此时方程的解组成的集合为{-1}；
当△＜0时，解得a＞1或a＜-
，此时方程的解组成的集合为∅．
当a≠0时，△=（a+1）2-4a2=-（3a+1）（a-1）．
当△＞0时，解得-
| 1 |
| 3 |
(a+1)±
| ||
| 2a |
此时方程的解组成的集合为{
a+1+
| ||
| 2a |
a+1-
| ||
| 2a |
当△=0时，解得a=-
| 1 |
| 3 |
| 1 |
| 3 |
当△＜0时，解得a＞1或a＜-
| 1 |
| 3 |
点评：本题考查了一元二次方程的解法、一元二次不等式的解法，考查了分类讨论的思想方法，考查了推理能力和计算能力，属于中档题．
练习册系列答案
提分百分百检测卷系列答案
相关题目
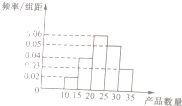为了调查某厂数万名工人独立生产某种产品的能力，随机抽查了m位工人某天独立生产该产品的数量，产品数量的分组区间为[10，15），[15，20），[20，25），[25，30），[30，35），频率分布直方图如图所示，已知独立生产的产品数量在[20，25）之间的工人有6位．
某校高三年段共有1000名学生，将其按专业发展取向分成普理、普文、艺体三类，如图是这三类的人数比例示意图．为开展某项调查，采用分层抽样的方法从这1000名学生中抽取一个容量为10的样本．