题目内容
已知函数f（x）=2cos2x+2
sinxcosx+1．
（Ⅰ）求函数f（x）的单调递增区间，最小正周期；
（Ⅱ）画出f（x）的图象．（要求：列表，要有超过一个周期的图象，并标注关键点）
| 3 |
（Ⅰ）求函数f（x）的单调递增区间，最小正周期；
（Ⅱ）画出f（x）的图象．（要求：列表，要有超过一个周期的图象，并标注关键点）
考点：三角函数中的恒等变换应用,五点法作函数y=Asin（ωx+φ）的图象
专题：三角函数的图像与性质
分析：（Ⅰ）利用二倍角公式和两角和公式对函数解析式化简，根据正弦函数的性质求得单调增区间和最小正周期．
（Ⅱ）利用五点描点法画图．
（Ⅱ）利用五点描点法画图．
解答：
解：（Ⅰ）f（x）=
sin2x+cos2x+2=2sin（2x+
）+2，
由2kπ-
≤2x+
≤2kπ+
，得kπ-
≤x≤kπ+
，k∈Z，
即函数的单调增区间为[kπ-
，kπ+
]（k∈Z），
T=
=π．
（Ⅱ）
| 3 |
| π |
| 6 |
由2kπ-
| π |
| 2 |
| π |
| 6 |
| π |
| 2 |
| π |
| 3 |
| π |
| 6 |
即函数的单调增区间为[kπ-
| π |
| 3 |
| π |
| 6 |
T=
| 2π |
| 2 |
（Ⅱ）
| x | -
|
|
|
|
| ||||||||||
2x+
| 0 |
| π |
| 2π | ||||||||||
| y | 2 | 4 | 2 | 0 | 2 |
点评：本题主要考查了三角函数图象与性质，三角函数恒等变换的应用．考查了学生基础知识的综合运用．
练习册系列答案
小学期末标准试卷系列答案
相关题目
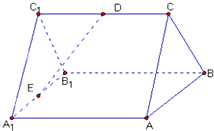如图，已知ABC-A1B1C1是正三棱柱，它的底面边长和侧棱长都是2，D为侧棱CC1的中点，E为底面一边A1B1的中点．
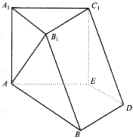如图，在六面体A1B1C1D1中，平面A1B1C1∥平面ABDE，△A1B1C1是正三角形，四边形AA1B1B是直角梯形，AB⊥AA1，四边形AEC1A1为正方形，四边形ABDE是等腰梯形，AB∥DE，AB=2AE=2DE=2．
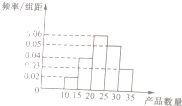为了调查某厂数万名工人独立生产某种产品的能力，随机抽查了m位工人某天独立生产该产品的数量，产品数量的分组区间为[10，15），[15，20），[20，25），[25，30），[30，35），频率分布直方图如图所示，已知独立生产的产品数量在[20，25）之间的工人有6位．
某校高三年段共有1000名学生，将其按专业发展取向分成普理、普文、艺体三类，如图是这三类的人数比例示意图．为开展某项调查，采用分层抽样的方法从这1000名学生中抽取一个容量为10的样本．