题目内容

在平面直角坐标系xOy中，已知曲线C1：
x2
3
+
y2
4
=1，以O为极点，x轴的正半轴极轴，取相同的单位长度建立极坐标系，直线l的方程为：ρ（2cosθ-sinθ）=6．
（1）试写出直线l的直角坐标方程和曲线C1的参数方程；
（2）在曲线C1上求一点P，使点P到直线l的距离最大，并求出最大值．
考点：简单曲线的极坐标方程
专题：坐标系和参数方程
分析：（1）根据x=ρcosθ，y=ρsinθ把直线l的极坐标方程化为直角坐标方程，利用同角三角函数的基本关系把曲线C1的直角坐标方程化为参数方程．
（2）设点P（
3
cosθ，2sinθ），求得点P到直线l的距离为d=
|4sin(
π
3
-θ)-6|
5
，利用正弦函数的值域求得d的最大值．
解答： 解：（1）直线l的方程为：ρ（2cosθ-sinθ）=6，即 2x-y-6=0．
曲线C1：
x2
3
+
y2
4
=1的参数方程为
x=
3
cosθ
y=2sinθ
（θ为参数）．
（2）设点P（
3
cosθ，2sinθ），则点P到直线l的距离为d=
|2
3
cosθ-2sinθ-6|
5
=
|4sin(
π
3
-θ)-6|
5
，
故当sin（
π
3
-θ）=-1时，d取得最大值为
10
5
=2
5
．
点评：本题主要考查把极坐标方程化为直角坐标方程的方法，点到直线的距离公式的应用，两角和的正弦公式、正弦函数的值域，属于基础题．
练习册系列答案
相关题目
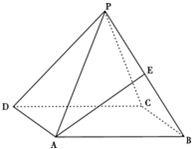正四棱锥P-ABCD中，侧面与底面ABCD所成的角为60°，E是PB的中点，求异面直线PD与AE所成角的大小．
极坐标系与直角坐标系xOy有相同的长度单位，以坐标原点O为极点，以x轴的正半轴为极轴，已知曲线C的极坐标方程为
1
ρ2
=
cos2θ
4
+sin2θ．
（1）将曲线C的极坐标方程化为参数方程；
（2）已知曲线C上两点A（ρ1，θ），B（ρ2，θ+
π
2
）（θ∈[0，π]），求△AOB面积的最小值及此时θ的值．
已知数列{an}满足a1=2，an+1=2an+2n+2；
（1）求a2，a3的值并证明数列{
an
2n
}为等差数列；
（2）bn=（-1）n+1
an
2n
，Tn=b1+b2+…+bn，求T51及Tn；
（3）令Cn=|
1
bnbn+1
|，Mn=C1+C2+…+Cn，求Mn的值．
已知数列{an}中，Sn是它的前n项和，并且2an是Sn+1与-2的等差中项，a1=1，
（1）设bn=an+1-2an（n=1，2，…），求证：数列{bn}是等比数列；
（2）求数列{an}的通项式；
（3）求数列{an}的前n项和公式．
某种产品的质量以其质量指标值衡量，质量指标值越大表明质量越好，且质量指标值大于或等于105的产品为优质品．现用两种新配方（分别称为甲配方和乙配方）做试验，各生产了100件这种产品，并测量了每件产品的质量指标值，得到如图所示试验结果．
（1）分别估计用甲配方，乙配方生产的产品的优质品率；
（2）已知用乙配方生产的一件产品的利润y（单位：元）与其质量指标值t的关系式为y=
-3 ，t＜95
3 ， 95≤t＜105
5， t≥105
，从用乙配方生产的产品中任取一件，其利润记为X（单位：元）求X的分布列及数学期望．（以试验结果中质量指标值落入各组的频率作为一件产品的质量指标值落入相应组的概率）
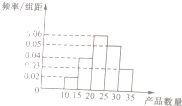为了调查某厂数万名工人独立生产某种产品的能力，随机抽查了m位工人某天独立生产该产品的数量，产品数量的分组区间为[10，15），[15，20），[20，25），[25，30），[30，35），频率分布直方图如图所示，已知独立生产的产品数量在[20，25）之间的工人有6位．
（Ⅰ）求m的值；
（Ⅱ）工厂规定：若独立生产产品数量当日不小于25，则该工人当选“生产之星”，若将这天独立生产该产品数量的频率视为概率，随机从全厂工人中抽取3人，这3人中当日“生产之星”人数为X，求X的分布列及数学期望E（X）．
（1）已知中心在原点的双曲线C的右焦点为（2，0），实轴长为2
3
．求双曲线C的方程．
（2）设抛物线y2=mx（m≠0）的准线与直线x=-1的距离为2，求抛物线的方程．
已知函数f（x）=
1
10
x+1，x≤1
lnx-1，x＞1
，若方程f（x）=ax恰有两个不同实数根，则实数a的取值范围是
 
．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网