题目内容
甲乙两个盒子里各放有标号为1,2,3,4的四个大小形状完全相同的小球,从甲盒中任取一小球,记下号码x后放入乙盒,再从乙盒中任取一小球,记下号码y,设随机变量X=|x-y|.
(1)求y=2的概率;
(2)求随机变量X的分布列及数学期望.
(1)求y=2的概率;
(2)求随机变量X的分布列及数学期望.
考点:离散型随机变量的期望与方差,古典概型及其概率计算公式
专题:概率与统计
分析:(1)由题意知y=2 包括两种情况,一是x=2,y=2,一是x≠2,y=2,根据变量的结果对应的事件做出两种情况的概率,这两种情况是互斥的,且每一种情况中包含的事件是相互独立事件,根据公式得到结果.
(2)由题意知随机变量的取值是0、1、2、3,根据不同变量对应的事件得到概率,写出分布列和期望.
(2)由题意知随机变量的取值是0、1、2、3,根据不同变量对应的事件得到概率,写出分布列和期望.
解答:
解:(1)由题意知y=2 包括两种情况:
一是x=2,y=2,一是x≠2,y=2,
∴P(y=2)=P(x=2,y=2)+P(x≠2,y=2)=
×
+
×
=
.
(2)随机变量X可取的值为0,1,2,3
当X=0时,(x,y)=(1,1),(2,2),(3,3),(4,4)
∴P(x=0)=
×
+
×
+
×
+
×
=
,
当X=1时,(x,y)=(1,2),(2,1),(2,3),(3,2),(3,4),(4,3)
∴P(X=1)=
×
+
×
+
×
+
×
+
×
+
×
=
,
同理,得P(X=2)=
,P(X=3)=
,
∴X的分布列:
∴EX=1×
+2×
+3×
=1.
一是x=2,y=2,一是x≠2,y=2,
∴P(y=2)=P(x=2,y=2)+P(x≠2,y=2)=
| 1 |
| 4 |
| 2 |
| 5 |
| 3 |
| 4 |
| 1 |
| 5 |
| 1 |
| 4 |
(2)随机变量X可取的值为0,1,2,3
当X=0时,(x,y)=(1,1),(2,2),(3,3),(4,4)
∴P(x=0)=
| 1 |
| 4 |
| 2 |
| 5 |
| 1 |
| 4 |
| 2 |
| 5 |
| 1 |
| 4 |
| 2 |
| 5 |
| 1 |
| 4 |
| 2 |
| 5 |
| 2 |
| 5 |
当X=1时,(x,y)=(1,2),(2,1),(2,3),(3,2),(3,4),(4,3)
∴P(X=1)=
| 1 |
| 4 |
| 1 |
| 5 |
| 1 |
| 4 |
| 1 |
| 5 |
| 1 |
| 4 |
| 1 |
| 5 |
| 1 |
| 4 |
| 1 |
| 5 |
| 1 |
| 4 |
| 1 |
| 5 |
| 1 |
| 4 |
| 1 |
| 5 |
| 3 |
| 10 |
同理,得P(X=2)=
| 1 |
| 5 |
| 1 |
| 10 |
∴X的分布列:
| X | 0 | 1 | 2 | 3 | ||||||||
| P |
|
|
|
|
| 3 |
| 10 |
| 1 |
| 5 |
| 1 |
| 10 |
点评:本题考查离散型随机变量的分布列和期望,这种类型是近几年高考题中经常出现的,考查离散型随机变量的分布列和期望,大型考试中理科考试必出的一道大题,文科考概率一般考查古典概型和几何概型.

练习册系列答案
 七彩题卡口算应用一点通系列答案
七彩题卡口算应用一点通系列答案
相关题目
若tanα=
,则
的值为( )
| 1 |
| 3 |
| sinα+cosα |
| sinα-cosα |
| A、1 | B、-1 | C、2 | D、-2 |
已知三棱锥的三视图如图所示,其中侧视图为直角三角形,俯视图为等腰直角三角形,则此三棱锥的体积等于( )


A、
| ||||
B、
| ||||
C、
| ||||
D、
|
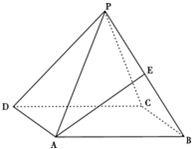 正四棱锥P-ABCD中,侧面与底面ABCD所成的角为60°,E是PB的中点,求异面直线PD与AE所成角的大小.
正四棱锥P-ABCD中,侧面与底面ABCD所成的角为60°,E是PB的中点,求异面直线PD与AE所成角的大小.
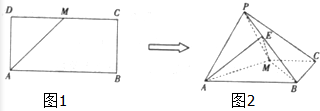 如图,已知长方形ABCD中,AB=2,AD=1,M为DC的中点.将△ADM沿AM折起到△APM,使得平面APM⊥平面ABCM,点E在线段PB上,且PE=
如图,已知长方形ABCD中,AB=2,AD=1,M为DC的中点.将△ADM沿AM折起到△APM,使得平面APM⊥平面ABCM,点E在线段PB上,且PE=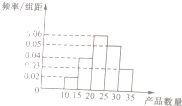 为了调查某厂数万名工人独立生产某种产品的能力,随机抽查了m位工人某天独立生产该产品的数量,产品数量的分组区间为[10,15),[15,20),[20,25),[25,30),[30,35),频率分布直方图如图所示,已知独立生产的产品数量在[20,25)之间的工人有6位.
为了调查某厂数万名工人独立生产某种产品的能力,随机抽查了m位工人某天独立生产该产品的数量,产品数量的分组区间为[10,15),[15,20),[20,25),[25,30),[30,35),频率分布直方图如图所示,已知独立生产的产品数量在[20,25)之间的工人有6位.