题目内容
已知数列{an}的各项都为正数，a1=1，前n项和Sn满足Sn-Sn-1=
+
（n≥2），试用数学归纳法求数列{an}的通项公式．
| Sn |
| Sn-1 |
考点：数学归纳法
专题：点列、递归数列与数学归纳法
分析：由已知可得，Sn-Sn-1=
+
（n≥2），结合等差数列的通项公式可求sn，进而可求an．然后利用数学归纳法的证明步骤证明即可．
| Sn |
| Sn-1 |
解答：
解：∵an=Sn-Sn-1=
+
，
∴Sn-Sn-1=（
+
）（
-
）=
+
．
∴
-
=1，
∴数列{
}是首项为1，公差为1的等差数列，
∴
=n，
∴sn=n2，∴an=
+
=n+n-1=2n-1（n≥2）
当n=1时，a1=1也适合，
∴an=2n-1．
用数学归纳法证：
①当n=1时，结论显然成立．
②假设当n=k时结论成立，即ak=2k-1.
=k，
则当n=k+1时，ak+1=
+
=
+k，解得ak+1=2k+1，
故当n=k+1时结论也成立．
由①、②可知，对于任意的n∈N*，都有an=n+1成立．
| Sn |
| Sn-1 |
∴Sn-Sn-1=（
| Sn |
| Sn-1 |
| Sn |
| Sn-1 |
| Sn |
| Sn-1 |
∴
| Sn |
| Sn-1 |
∴数列{
| Sn |
∴
| Sn |
∴sn=n2，∴an=
| Sn |
| Sn-1 |
当n=1时，a1=1也适合，
∴an=2n-1．
用数学归纳法证：
①当n=1时，结论显然成立．
②假设当n=k时结论成立，即ak=2k-1.
| Sk |
则当n=k+1时，ak+1=
| Sk+1 |
| Sk |
| k2+ak+1 |
故当n=k+1时结论也成立．
由①、②可知，对于任意的n∈N*，都有an=n+1成立．
点评：本题主要考查了利用数列的递推公式构造等差数列求数列的通项公式．数学归纳法z的证明步骤，第（1）问要注意递推公式的灵活运用，第（2）问要注意数学归纳法的证明技巧．数学归纳法的基本形式设P（n）是关于自然数n的命题，若1°P（n0）成立2°假设P（k）成立（k≥n0），可以推出P（k+1）成立，则P（n）对一切大于等于n0的自然数n都成立．
练习册系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目
已知三棱锥的三视图如图所示，其中侧视图为直角三角形，俯视图为等腰直角三角形，则此三棱锥的体积等于（ ）
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
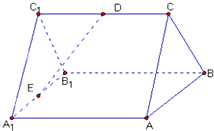如图，已知ABC-A1B1C1是正三棱柱，它的底面边长和侧棱长都是2，D为侧棱CC1的中点，E为底面一边A1B1的中点．
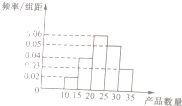为了调查某厂数万名工人独立生产某种产品的能力，随机抽查了m位工人某天独立生产该产品的数量，产品数量的分组区间为[10，15），[15，20），[20，25），[25，30），[30，35），频率分布直方图如图所示，已知独立生产的产品数量在[20，25）之间的工人有6位．