题目内容
△ABC中，∠A，∠B，∠C所对的边分别为a，b，c，若a=3，b=4，∠C=60°，则c的值等于（ ）
| A、5 | ||
| B、13 | ||
C、
| ||
D、
|
考点：余弦定理
专题：解三角形
分析：利用余弦定理列出关系式，把a，b，cosC的值代入求出c的值即可．
解答：
解：∵△ABC中，a=3，b=4，∠C=60°，
∴由余弦定理得：c2=a2+b2-2abcosC=9+16-12=13，
则c=
．
故选：C．
∴由余弦定理得：c2=a2+b2-2abcosC=9+16-12=13，
则c=
| 13 |
故选：C．
点评：此题考查了余弦定理，以及特殊角的三角函数值，熟练掌握余弦定理是解本题的关键．
练习册系列答案
名校课堂系列答案
相关题目
在△ABC中，∠A=30°，AB=4，满足此条件的△ABC有两解，则BC边长度的取值范围为（ ）
A、（2
| ||
| B、（2，4） | ||
| C、（4，+∞） | ||
D、（2
|
若曲线y=
与直线y=kx+1有两个不同的交点，则实数k的取值范围是（ ）
|
A、(-3-2
| ||||
B、(-3+2
| ||||
C、(-∞，-3-2
| ||||
D、(-3-2
|
已知点已知点P（8，8）在抛物线C：y2=2px（p＞0）上，直线l与抛物线C相切于点P，则直线l的斜率为（ ）
A、
| ||
B、
| ||
C、
| ||
D、
|
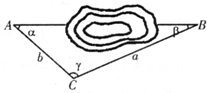如图，为了测量隧道两口之间AB的长度，对给出的四组数据，求解计算时，较为简便易行的一组是（ ）| A、a，b，γ |
| B、a，b，α |
| C、a，b，β |
| D、α，β，a |