题目内容
若曲线y=
与直线y=kx+1有两个不同的交点,则实数k的取值范围是( )
|
A、(-3-2
| ||||
B、(-3+2
| ||||
C、(-∞,-3-2
| ||||
D、(-3-2
|
考点:函数的零点与方程根的关系
专题:函数的性质及应用
分析:作出两个函数的图象,利用数形结合即可得到结论.
解答:
解:作出曲线y=
的图象如图:
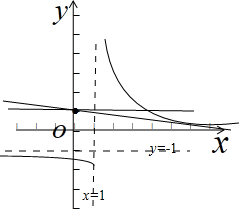
直线y=kx+1过定点(0,1),
当k=0时,两个函数只有一个交点,不满足条件,
当k>0时,两个函数有2个交点,满足条件,
当k<0时,直线y=kx+1与y=
在x>1相切时,两个函数只有一个交点,
此时
=kx+1,即kx2+(1-k)x-2=0,
判别式△=(1-k)2+8k=0,k2+6k+1=0,
解得:k=-3+2
,或k=-3-2
(舍去),
则此时满足-3+2
<k<0,
综上满足条件的k的取值范围是(-3+2
,0)∪(0,+∞),
故选:B.
|

直线y=kx+1过定点(0,1),
当k=0时,两个函数只有一个交点,不满足条件,
当k>0时,两个函数有2个交点,满足条件,
当k<0时,直线y=kx+1与y=
| 1 |
| x-1 |
此时
| 1 |
| x-1 |
判别式△=(1-k)2+8k=0,k2+6k+1=0,
解得:k=-3+2
| 2 |
| 2 |
则此时满足-3+2
| 2 |
综上满足条件的k的取值范围是(-3+2
| 2 |
故选:B.
点评:本题主要考查函数与方程的应用,利用数形结合以及分段函数的性质是解决本题的关键.

练习册系列答案
相关题目
△ABC中,∠A,∠B,∠C所对的边分别为a,b,c,若a=3,b=4,∠C=60°,则c的值等于( )
| A、5 | ||
| B、13 | ||
C、
| ||
D、
|
下列命题中正确的是( )
| A、一直线与一平面平行,这个平面内有无数条直线与它平行 |
| B、平行于同一直线的两个平面平行 |
| C、与两相交平面的交线平行的直线必平行于这两个相交平面 |
| D、两条平行直线中的一条与一个平面平行,则另一条也与该平面平行 |
已知椭圆
+
=1上一点A(2,1)和该椭圆上两动点B、C,直线AB、AC的斜率分别为k1、k2,且k1+k2=0,则直线BC的斜率k( )
| x2 |
| 8 |
| y2 |
| 2 |
A、k>
| ||||
B、k=-
| ||||
C、k=
| ||||
| D、k的值不确定 |
 如图,四棱锥P-ABCD中,PA⊥平面ABCD,AB∥CD,∠BAD=∠ADC=90°,AB=AD=2CD,E为PB的中点.
如图,四棱锥P-ABCD中,PA⊥平面ABCD,AB∥CD,∠BAD=∠ADC=90°,AB=AD=2CD,E为PB的中点.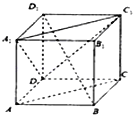 如图正方体ABCD-A1B1C1D1,下面结论正确的是
如图正方体ABCD-A1B1C1D1,下面结论正确的是