题目内容
 已知点P(1,-
已知点P(1,-| 3 |
| 2 |
| x2 |
| a2 |
| y2 |
| b2 |
(1)求椭圆C的方程;
(2)直线l过点T(m,0)交椭圆C于M、N两点,AB是椭圆C经过原点O的弦,且MN∥AB,问是否存在正数m,使
| |AB|2 |
| |MN| |
考点:直线与圆锥曲线的综合问题
专题:综合题,圆锥曲线的定义、性质与方程
分析:(1)利用椭圆的定义求出a=2,再求出b,由此能求出椭圆的标准方程.
(2)分类讨论,当直线斜率存在时,设直线l的方程为y=k(x-m)(k≠0),M(x1,y1),N(x2,y2),由直线y=k(x-m)代入椭圆方程,消去y可得(3+4k2)x2-8k2mx+4k2m2-12=0,再由韦达定理,求出|MN|,同理求出|AB|,即可得出结论.
(2)分类讨论,当直线斜率存在时,设直线l的方程为y=k(x-m)(k≠0),M(x1,y1),N(x2,y2),由直线y=k(x-m)代入椭圆方程,消去y可得(3+4k2)x2-8k2mx+4k2m2-12=0,再由韦达定理,求出|MN|,同理求出|AB|,即可得出结论.
解答:
解:(1)椭圆C的左焦点为(1,0),∴c=1,椭圆C的右焦点为(-1,0)
可得2a=
+
=
+
=4,解得a=2,…(2分)
∴b2=a2-c2=4-1=3,
∴椭圆C的标准方程为
+
=1…(4分)
(2)设直线l:y=k(x-m),且M(x1,y1),N(x2,y2),由
得(3+4k2)x2-8k2mx+4k2m2-12=0,
∴x1+x2=
,x1x2=
…(7分)
∴|MN|=
…(10分)
由
得x2=
设A(x3,y3),B(x4,y4)
得|AB|=
|x3-x4|得|AB|2=
…(12分)
而64k4m2-16(3+4k2)(k2m2-3)=16[(12-3m2)k2+9]
∴当12-3m2=9即m=1时
=4为定值,当k不存在时,定值也为4,
∴m=1…(15分)
可得2a=
(1+1)2+(-
|
(1-1)2+(-
|
| 5 |
| 2 |
| 3 |
| 2 |
∴b2=a2-c2=4-1=3,
∴椭圆C的标准方程为
| x2 |
| 4 |
| y2 |
| 3 |
(2)设直线l:y=k(x-m),且M(x1,y1),N(x2,y2),由
|
得(3+4k2)x2-8k2mx+4k2m2-12=0,
∴x1+x2=
| 8k2m |
| 3+4k2 |
| 4k2m2-12 |
| 3+4k2 |
∴|MN|=
| ||||
| 3+4k2 |
由
|
| 12 |
| 3+4k2 |
设A(x3,y3),B(x4,y4)
得|AB|=
| 1+k2 |
| 48(1+k2) |
| 3+4k2 |
而64k4m2-16(3+4k2)(k2m2-3)=16[(12-3m2)k2+9]
∴当12-3m2=9即m=1时
| |AB|2 |
| |MM| |
∴m=1…(15分)
点评:本题考查椭圆的方程,直线与椭圆的位置关系,考查韦达定理的运用,考查学生的计算能力,属于中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
定义在实数集R上的函数y=f(x)的图象是连续不断的,若对任意的实数,存在常数使得f(t+x)=-tf(x)恒成立,则称f(x)是一个“关于t函数”,下列“关于t函数”的结论正确的是( )
| A、f(x)=2不是“关于t函数” | ||
| B、f(x)=x是一个“关于t函数” | ||
C、“关于
| ||
| D、f(x)=sinπx不是一个“关于t函数” |
△ABC中,∠A,∠B,∠C所对的边分别为a,b,c,若a=3,b=4,∠C=60°,则c的值等于( )
| A、5 | ||
| B、13 | ||
C、
| ||
D、
|
A,B,C为△ABC三内角,则“cosA+sinA=cosB+sinB”是“∠C=90°”的( )
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充要条件 |
| D、既不充分又不必要条件 |
已知双曲线
-
=1(a>0,b>0)的一条渐近线方程是y=
x,它的一个焦点在抛物线y2=24x的准线上,则双曲线的方程为( )
| x2 |
| a2 |
| y2 |
| b2 |
| 3 |
A、x2-
| ||||
B、
| ||||
C、
| ||||
D、
|
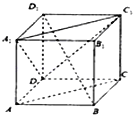 如图正方体ABCD-A1B1C1D1,下面结论正确的是
如图正方体ABCD-A1B1C1D1,下面结论正确的是 已知直角梯形ABCD和矩形CDEF所在的平面互相垂直,AD⊥DC,AB∥DC,AB=AD=DE=4,DC=8,
已知直角梯形ABCD和矩形CDEF所在的平面互相垂直,AD⊥DC,AB∥DC,AB=AD=DE=4,DC=8,