题目内容
若复数z满足z=i(2+z)(i为虚数单位),则z= .
考点:复数代数形式的乘除运算
专题:数系的扩充和复数
分析:根据复数的基本运算进行求解即可.
解答:
解:由z=i(2+z)=zi+2i得(1-i)z=2i,
则z=
=
=
=-1+i,
故答案为:-1+i
则z=
| 2i |
| 1-i |
| 2i(1+i) |
| (1+i)(1-i) |
| -2+2i |
| 2 |
故答案为:-1+i
点评:本题主要考查复数的基本运算,比较基础.

练习册系列答案
相关题目
已知函数f(x)的导函数的图象如图所示,则下列判断中正确的是( )
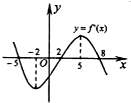

| A、函数f(x)在区间(-2,2)内单调递增 |
| B、函数f(x)在区间(-5,2)内单调递减 |
| C、函数f(x)在区间(5,8)内单调递减 |
| D、函数f(x)在区间(-2,5)内为单调函数 |
a=40.3,b=0.34,c=log40.3,d=log0.34则( )
| A、a>b>d>c |
| B、a>b>c>d |
| C、a<b<d<c |
| D、c<b<d<a |