题目内容
求函数y=
log
2x+log
x+5在区间[2,8]上的最大值和最小值.
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
考点:函数的最值及其几何意义
专题:计算题,函数的性质及应用
分析:令log
x=t,根据x的范围求出t的范围,转化成关于t的二次函数,然后进行配方得到对称轴,根据二次函数的性质可求出函数y的最值,然后求出相应的x即可.
| 1 |
| 2 |
解答:
解:令log
x=t,x∈[2,8]则t∈[-3,-1]
∴y=
t2+t+5=
(t+1)2+
①当t=-3,即x=8时,ymin=
,
②当t=-1,即x=2时,ymax=
.
| 1 |
| 2 |
∴y=
| 1 |
| 2 |
| 1 |
| 2 |
| 9 |
| 2 |
①当t=-3,即x=8时,ymin=
| 13 |
| 2 |
②当t=-1,即x=2时,ymax=
| 9 |
| 2 |
点评:本题主要考查了对数的运算性质,同时考查了换元法的应用,转化与划归的数学思想,属于基础题.

练习册系列答案
 英才计划期末调研系列答案
英才计划期末调研系列答案 精英口算卡系列答案
精英口算卡系列答案
相关题目
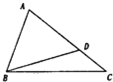 如图,在△ABC中,sin
如图,在△ABC中,sin