题目内容
曲线f（x）=ex（其中e为自然对数的底数）在点（0，1）处的切线与直线y=-x+3和x轴所围成的区域D（包含边界），点P（x，y）为区域D内的动点，则z=x-3y的最大值为（ ）
| A、3 | B、4 | C、-1 | D、2 |
考点：利用导数研究曲线上某点切线方程
专题：计算题,导数的概念及应用
分析：求出函数f（x）的导数，求出切线的斜率，写出切线方程，画出可行域D，画出直线l0，将它平移观察经过点（3，0）时取得最大值，求出即可．
解答：
解：f（x）=ex的导数为f′（x）=ex，
在点（0，1）处的切线斜率为e0=1，
则切线方程为：y=x+1，由
求出交点为（1，2），
如图画出区域D，作出直线l0：x-3y=0，
平移直线l0，观察当经过点（3，0）时，
z=x-3y取最大值3．
故选：A．
解：f（x）=ex的导数为f′（x）=ex，在点（0，1）处的切线斜率为e0=1，
则切线方程为：y=x+1，由
|
求出交点为（1，2），
如图画出区域D，作出直线l0：x-3y=0，
平移直线l0，观察当经过点（3，0）时，
z=x-3y取最大值3．
故选：A．
点评：本题主要考查导数的几何意义及应用，求切线方程，同时考查线性规划应用于求目标函数的最值，是一道基础题．
练习册系列答案
优加精卷系列答案
相关题目
复数z=-2+i，则它的共轭复数
在复平面内对应的点位于（ ）
. |
| z |
| A、第一象限 | B、第二象限 |
| C、第三象限 | D、第四象限 |
“x≥1”是“x+
≥2”（ ）
| 1 |
| x |
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充分且必要条件 |
| D、既不充分也不必要条件 |
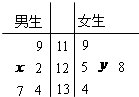某数学兴趣小组有男女生各5名．以下茎叶图记录了该小组同学在一次数学测试中的成绩（单位：分）．已知男生数据的中位数为125，女生数据的平均数为126.8．