题目内容
已知函数f(x)=ln(x+a)-x有且只有一个零点,其中a>0.
(Ⅰ)求a的值;
(Ⅱ)若对任意的x∈(0,+∞),有f(x)≥kx2成立,求实数k的最大值;
(Ⅲ)设h(x)=f(x)+x,对任意x1,x2∈(-1,+∞)(x1≠x2),证明:不等式
>
恒成立.
(Ⅰ)求a的值;
(Ⅱ)若对任意的x∈(0,+∞),有f(x)≥kx2成立,求实数k的最大值;
(Ⅲ)设h(x)=f(x)+x,对任意x1,x2∈(-1,+∞)(x1≠x2),证明:不等式
| x1-x2 |
| h(x1)-h(x2) |
| x1x2+x1+x2+1 |
考点:函数零点的判定定理,函数恒成立问题
专题:导数的综合应用
分析:(Ⅰ)通过求导得到单调区间找到极值点代入即可,(Ⅱ)由k≥0时不合题意.当k<0时令g'(x)=0通过讨论得出k的值,
(Ⅲ)不妨设x1>x2>-1,引进新函数找到其单调区间,问题得证.
(Ⅲ)不妨设x1>x2>-1,引进新函数找到其单调区间,问题得证.
解答:
解:(Ⅰ)f(x)的定义域为(-a,+∞),f′(x)=
-1=-
.
由f'(x)=0,得x=1-a>-a.
∵当-a<x<1-a时,f'(x)>0;当x>1-a时,f'(x)<0,
∴f(x)在区间(-a,1-a]上是增函数,在区间[1-a,+∞)上是减函数,
∴f(x)在x=1-a处取得最大值.
由题意知f(1-a)=-1+a=0,解得a=1.
(Ⅱ)由(Ⅰ)知f(x)=ln(x+1)-x,
当k≥0时,取x=1得,f(1)=ln2-1<0,知k≥0不合题意.
当k<0时,设g(x)=f(x)-kx2=ln(x+1)-x-kx2.
则g′(x)=
-1+2kx=
.
令g'(x)=0,得x1=0,x2=-
=-1-
>-1.
①若x2=-
≤0,即k≤-
时,g'(x)>0在x∈(0,+∞)上恒成立,
∴g(x)在[0,+∞)上是增函数,从而总有g(x)≥g(0)=0,
即f(x)≥kx2在[0,+∞)上恒成立.
②若x2=-
>0,即-
<k<0时,对于x∈(0 , -
),g'(x)<0,
∴g(x)在(0 , -
)上单调递减.
于是,当取x0∈(0 , -
)时,g(x0)<g(0)=0,即f(x0)≥kx02不成立.
故-
<k<0不合题意.
综上,k的最大值为-
.
(Ⅲ) 由h(x)=f(x)+x=ln(x+1).
不妨设x1>x2>-1,则要证明
>
,
只需证明
>
,
即证
>ln
,
即证
>ln
.
设t=
(t>1),则只需证明
>lnt(t>1),
化简得
>lnt.
设φ(t)=
-lnt,则φ′(t)=
>0,
∴φ(t)在(1,+∞)上单调递增,
∴φ(t)>φ(1)=0.
即
>lnt,得证.
故原不等式恒成立.
| 1 |
| x+a |
| x+a-1 |
| x+a |
由f'(x)=0,得x=1-a>-a.
∵当-a<x<1-a时,f'(x)>0;当x>1-a时,f'(x)<0,
∴f(x)在区间(-a,1-a]上是增函数,在区间[1-a,+∞)上是减函数,
∴f(x)在x=1-a处取得最大值.
由题意知f(1-a)=-1+a=0,解得a=1.
(Ⅱ)由(Ⅰ)知f(x)=ln(x+1)-x,
当k≥0时,取x=1得,f(1)=ln2-1<0,知k≥0不合题意.
当k<0时,设g(x)=f(x)-kx2=ln(x+1)-x-kx2.
则g′(x)=
| 1 |
| x+1 |
| -x(2kx+2k+1) |
| x+1 |
令g'(x)=0,得x1=0,x2=-
| 2k+1 |
| 2k |
| 1 |
| 2k |
①若x2=-
| 2k+1 |
| 2k |
| 1 |
| 2 |
∴g(x)在[0,+∞)上是增函数,从而总有g(x)≥g(0)=0,
即f(x)≥kx2在[0,+∞)上恒成立.
②若x2=-
| 2k+1 |
| 2k |
| 1 |
| 2 |
| 2k+1 |
| 2k |
∴g(x)在(0 , -
| 2k+1 |
| 2k |
于是,当取x0∈(0 , -
| 2k+1 |
| 2k |
故-
| 1 |
| 2 |
综上,k的最大值为-
| 1 |
| 2 |
(Ⅲ) 由h(x)=f(x)+x=ln(x+1).
不妨设x1>x2>-1,则要证明
| x1-x2 |
| h(x1)-h(x2) |
| x1x2+x1+x2+1 |
只需证明
| (x1+1)-(x2+1) |
| ln(x1+1)-ln(x2+1) |
| (x1+1)(x2+1) |
即证
|
| x1+1 |
| x2+1 |
即证
|
| x1+1 |
| x2+1 |
设t=
| x1+1 |
| x2+1 |
t-2+
|
化简得
| t-1 | ||
|
设φ(t)=
| t-1 | ||
|
| (t-1)2 | ||
2t
|
∴φ(t)在(1,+∞)上单调递增,
∴φ(t)>φ(1)=0.
即
| t-1 | ||
|
故原不等式恒成立.
点评:本题考察了导函数,单调区间及最值,函数的零点,不等式的证明,是一道较难的综合题.

练习册系列答案
相关题目
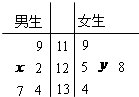 某数学兴趣小组有男女生各5名.以下茎叶图记录了该小组同学在一次数学测试中的成绩(单位:分).已知男生数据的中位数为125,女生数据的平均数为126.8.
某数学兴趣小组有男女生各5名.以下茎叶图记录了该小组同学在一次数学测试中的成绩(单位:分).已知男生数据的中位数为125,女生数据的平均数为126.8. 已知椭圆E:
已知椭圆E: