题目内容
已知向量
=(cos θ，sin θ)和
=(
-sin θ，cos θ)，θ∈（π，2π），且|
+
|=
，求cos(
+
)的值．
| m |
| n |
| 2 |
| m |
| n |
8
| ||
| 5 |
| θ |
| 2 |
| π |
| 8 |
考点：两角和与差的余弦函数,向量的模,同角三角函数基本关系的运用
专题：综合题,三角函数的图像与性质
分析：由题意可得
+
的坐标，由模长可得
（cosθ-sinθ）=
，由三角函数公式可得cos（θ+
）=
，结合角的范围可得cos(
+
)＜0，由二倍角公式可得2cos2(
+
)-1=
，解方程可得．
| m |
| n |
| 2 |
| 14 |
| 25 |
| π |
| 4 |
| 7 |
| 25 |
| θ |
| 2 |
| π |
| 8 |
| θ |
| 2 |
| π |
| 8 |
| 7 |
| 25 |
解答：
解：∵
=(cos θ，sin θ)，
=(
-sin θ，cos θ)，
∴
+
=（
+cosθ-sinθ，sinθ+cosθ）
∵|
+
|=
，∴|
+
|2=
，
∴（
+cosθ-sinθ）2+（sinθ+cosθ）2=
，
可得2+2
（cosθ-sinθ）+（cosθ-sinθ）2+（sinθ+cosθ）2=
，
展开化简可得
（cosθ-sinθ）=
，
即2cos（θ+
）=
，
解得cos（θ+
）=
，
∵θ∈（π，2π），∴
+
∈（
，
）∴cos(
+
)＜0
由二倍角公式可得cos（θ+
）=2cos2(
+
)-1=
，
解得cos(
+
)=-
| m |
| n |
| 2 |
∴
| m |
| n |
| 2 |
∵|
| m |
| n |
8
| ||
| 5 |
| m |
| n |
| 128 |
| 25 |
∴（
| 2 |
| 128 |
| 25 |
可得2+2
| 2 |
| 128 |
| 25 |
展开化简可得
| 2 |
| 14 |
| 25 |
即2cos（θ+
| π |
| 4 |
| 14 |
| 25 |
解得cos（θ+
| π |
| 4 |
| 7 |
| 25 |
∵θ∈（π，2π），∴
| θ |
| 2 |
| π |
| 8 |
| 5π |
| 8 |
| 9π |
| 8 |
| θ |
| 2 |
| π |
| 8 |
由二倍角公式可得cos（θ+
| π |
| 4 |
| θ |
| 2 |
| π |
| 8 |
| 7 |
| 25 |
解得cos(
| θ |
| 2 |
| π |
| 8 |
| 4 |
| 5 |
点评：本题考查三角函数的公式，涉及同角三角函数的基本关系以及向量的模长公式，属中档题．
练习册系列答案
期末好成绩系列答案
99加1领先期末特训卷系列答案
百强名校期末冲刺100分系列答案
好成绩1加1期末冲刺100分系列答案
金状元绩优好卷系列答案
相关题目
“x≥1”是“x+
≥2”（ ）
| 1 |
| x |
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充分且必要条件 |
| D、既不充分也不必要条件 |
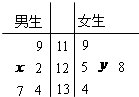某数学兴趣小组有男女生各5名．以下茎叶图记录了该小组同学在一次数学测试中的成绩（单位：分）．已知男生数据的中位数为125，女生数据的平均数为126.8．